Диффузией называют процесс самопроизвольного выравнивания концентраций в системе, приводящий к установлению одинакового химического потенциала каждого компонента во всех элементах объема системы.
Связь потока диффузии J с градиентом концентрации 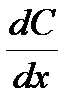 (он пропорционален градиенту химического потенциала) устанавливает первый закон Фика(*)
(он пропорционален градиенту химического потенциала) устанавливает первый закон Фика(*)
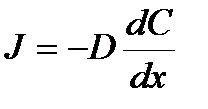 (3.3)
(3.3)
или
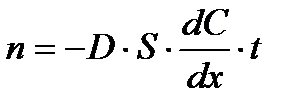 (3.4)
(3.4)
Диффузионный поток J численно равен количеству вещества n (числу моль), перенесенному диффузией за единицу времени t через единицу площади S сечения, перпендикулярного к направлению диффузии x.
Знак «минус» в уравнениях (3.3) и (3.4) поставлен потому, что поток по определению – величина положительная, а градиент концентрации отрицателен (J направлен в сторону уменьшения концентрации, т.е. dC < 0 при dx > 0).
Коэффициент пропорциональности D называют коэффициентом диффузии. Формально его физический смысл следует из уравнения (3.4).
D равен количеству вещества, перенесённого диффузией через 1 м2 поверхности за 1 с при единичном градиенте концентрации – скорость, с которой система выравнивает единичную разность концентрации.
Величина D является, таким образом, мерой интенсивности диффузии.
Измеряется D в м2/с или см2/с, порядок величины D для газов ~ 0.1 - 1 см2/с, для жидкостей 10-5 – 10-6см2/с, для коллоидных систем 10-7–10-10 см2/с (в зависимости от размера частиц и свойств среды).
Одновременно с диффузионным переносом растворённого вещества, неравномерно распределённого в среде (имеющего градиент концентрации), происходит самодиффузия – случайное перемещение частиц самой среды, химический состав которой при этом не изменяется. Данный процесс наблюдается при отсутствии градиента концентрации. Эффект самодиффузии может приводить к сращиванию двух пришлифованных образцов одного и того же вещества, спеканию порошков при пропускании через них электрического тока, к растягиванию тел под действием подвешенного к ним груза (диффузионная ползучесть материала).
В случае дисперсных систем движущей силой диффузии является броуновское движение, следовательно, должна быть связь между коэффициентом диффузии и средним квадратичным сдвигом 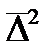 (количественная характеристика броуновского движения). Эту зависимость установил Эйнштейн:
(количественная характеристика броуновского движения). Эту зависимость установил Эйнштейн:
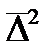 = 2×D×t (3.5)
= 2×D×t (3.5)
Отсюда следует и выражение для коэффициента диффузии, вытекающее из молекулярно – кинетической теории броуновского движения:
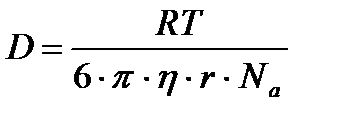 (3.6)
(3.6)
Основанные на общих положениях молекулярно-кинетической теории, уравнения (3.5) и (3.6) могут быть использованы для расчётов диффузии любых частиц: молекул газа и растворенных веществ, коллоидных частиц. Так, время прохождения фронтом диффундирующего вещества пути 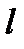 (соответствующего
(соответствующего 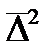 ) согласно (3.6) определяется как:
) согласно (3.6) определяется как: 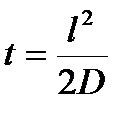
Для коллоидных частиц, характеризующихся значением D = 5×10-9 cм2/с, время прохождения фронтом частиц растояния 1 см составит около трех лет, тогда как для молекул - несколько часов.
Таким образом, для коллоидных систем характерна весьма медленная, но все же измеримая диффузия, позволяющая произвести определение размеров диффундирующих частиц.
Седиментация суспензий
В свободнодисперсных системах частицы дисперсной фазы могут перемещаться по всему объему системы. Частицы грубодисперсных систем (суспензий, эмульсий и др.) не участвуют в броуновском движении и в зависимости от соотношения плотностей частиц и среды либо осаждаются под действием силы тяжести, либо всплывают под действием силы Архимеда.
Процесс оседания частиц дисперсной фазы в жидкой или газообразной среде под действием силы тяжести называют седиментацией, а процесс всплытия - обратной седиментацией.
На частицы, находящиеся в жидкости действуют две силы
- сила тяжести F=mg
и выталкивающая сила - сила Архимеда(*) Fa.
Равнодействующая этих сил - сила, вызывающая седиментацию Fc. Она равна:
Fc = mg - Fa = V×r×g - V×ro×g = V×g×(r - ro), (3.7)
где V - объем частицы, g - ускорение силы тяжести, r и ro- плотности частиц и среды, соответственно.
Под действием Fc частицы начинают двигаться с ускорением, но по мере роста скорости увеличивается и сила сопротивления среды, пропорциональная скорости движения Fтр = B×U. Наконец, наступает момент, когда Fc становится равной Fтр и частица начинает двигаться равномерно с постоянной скоростью U:
V×g×(r - ro) = B×U и U = V×g×(r - ro)/B (3.8)
Здесь B - коэффициент трения среды. Для сферических частиц, движущихся ламинарно в жидкости, коэффициент B обычно выражают законом Стокса(*):
B = 6×p×h×r (3.9)
Тогда скорость равномерного движения равна:
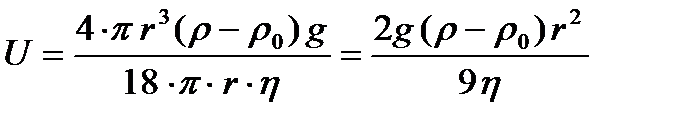 (3.10)
(3.10)
или
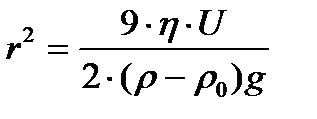 = K×U, (3.11)
= K×U, (3.11)
где h - вязкость жидкости, r - радиус частицы.
Скорость осаждения частиц можно рассчитать, зная путь частицы при осаждении H и время её осаждения t: U = H/t. Окончательно выражение для радиуса частиц имеет вид:
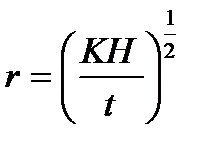 (3.12)
(3.12)
Это уравнение лежит в основе седиментационного анализа дисперсности грубодисперсных коллоидных систем, целью которого является установление минимального, максимального и наивероятнейшего радиусов частиц системы, а так же - распределения частиц по радиусам.
По такому закону происходит осаждение частиц в суспензиях, аэрозолях, эмульсиях.
Условия соблюдения законов седиментации
(зaкона Стокса)
1. Независимость осаждения частиц (разбавленные системы, иначе тормозится движение частиц из-за их столкновения).
2. Ламинарность движения
3. Дисперсность частиц от 0,1 мкм до 100 мкм, так как частицы с диаметром меньше 0,1 мкм обладают заметным броуновским движением, а частицы с диаметром, большим 100 мкм, движутся равноускоренно (возникает турбулентность).
4. Сферическая форма частиц. Частицы неправильной формы ориентируются в направлении движения. Для применения закона Стокса используют в этом случае понятие эквивалентного радиуса (т.е. радиуса сферы частиц, оседающих с той же скоростью, что и реальные частицы).
Способность к седиментации принято выражать через константу седиментации, которая определяется скоростью осаждения:
Sсед= V(ρ-ρo)/gВ= U/g (3.13)
Для сферических частиц Sсед=2 r2 (ρ-ρo)/9η, единица измерения – Сведберг(*): 1Сб=10-13 с.
Для аэрозолей, суспензий, эмульсий константа седиментации очень велика, поэтому используют мегаСведберги (МСб) или с. Для частиц кварца (радиус 10-3 см) Sсед = 3,25 10–5 с= 325 МСб=0,325 ГСб.
Таблица 3.1
Скорость седиментации сферических частиц SiO2 в H2O
| r частицы, мкм | 0,1 | 0,01 | 0,001 | ||
| Uсед, см/с | 3,6 10-2 | 3,610-4 | 3,610-6 | 3,610-8 | 3,610-10 |
| Время оседания на 1см | 28с | 46,5 мин | 77,5 ч | 323 дня | 89 лет |
