I Определения, формулы
Многогранник (многогранная поверхность) — поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
Грани — многоугольники, из которых составлен многогранник.
Ребра — стороны граней многогранника.
Вершины — концы ребер многогранника.
Диагональ — отрезок, соединяющий две вершины, не принадлежащие одной грани.
Сечение — общая часть многогранника и секущей плоскости.
Призма — многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Высота призмы — перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.
Прямая призма — призма, в которой боковые ребра перпендикулярны к основаниям.
Наклонная призма — призма, в которой боковые ребра не перпендикулярны к основаниям.
Правильная призма — прямая призма, основаниями которой являются правильные многоугольники.
Площадь полной поверхности призмы: 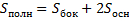
Пирамида — многогранник, составленный из n-угольника и n треугольников.
Высота пирамиды — перпендикуляр, проведенный из вершины пирамиды к плоскости основания.
Площадь полной поверхности пирамиды: 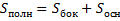
Правильная пирамида — пирамида, основанием которой является правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является высотой.
Усеченная пирамида — многогранник, гранями которого являются два n-угольника (верхнее и нижнее основания), расположенные в параллельных плоскостях, и n четырехугольников (боковых граней).
Правильная усеченная пирамида — пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию.
Правильный выпуклый многогранник — выпуклый многогранник, все грани которого являются равными правильными многоугольниками и в каждой вершине которого сходится одно и то же количество ребер.
II Вопросы
1. Какое наименьшее число ребер может иметь многогранник?
Наименьшее число ребер имеет тетраэдр — 6.
2. Призма имеет n граней. Какой многоугольник лежит в её основании?
n-угольник
3. Является ли призма прямой, если 2 её смежные боковые грани перпендикулярны к плоскости основания?
Да, является, т. к. если боковые ребра призмы перпендикулярны основанию, то призма называется прямой.
4. В какой призме боковые ребра параллельны её высоте?
В прямой призме, т. к. высота перпендикулярна основанию, так же как и боковые ребра прямой призмы перпендикулярны основанию. «Если две прямые перпендикулярны плоскости, то они параллельны».
5. Является ли призма правильной, если все её ребра равны друг другу?
Да, т. к. в правильной призме все боковые грани — равные прямоугольники —> боковые ребра равны.
6. Может ли высота одной из боковых граней наклонной призмы являться и высотой призмы?
Да, если эта грань перпендикулярна основанию призмы.
7. Существует ли призма, у которой:
а) боковое ребро перпендикулярно только одному ребру основания?
Да, в наклонной призме.
б) только одна боковая грань перпендикулярна основанию?
Нет. Если боковая грань перпендикулярна основанию, значит, призма прямая —> все боковые грани перпендикулярны основанию.
Правильная треугольная призма разбивается плоскостью, проходящей через средние линии оснований, на две призмы. Как относятся площади боковых поверхностей этих призм?
Формула площади боковой поверхности: 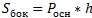 . Высоты равны —>
. Высоты равны —> 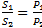 .
.  ;
; 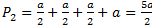 —>
—> 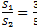 .
.
9. Будет ли пирамида правильной, если её боковыми гранями являются правильные треугольники?
Да, будет, т. к. все боковые грани правильной пирамиды — равные равнобедренные треугольники.
10. Сколько граней, перпендикулярных к плоскости основания, может иметь пирамида?
Две. Рисуем треугольник/квадрат и две грани перпендикулярные основанию.
11. Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основанию?
Нет, перпендикулярны к основанию могут быть только две смежные грани. Иначе бы через вершину пирамиды проходили бы как минимум две прямые, перпендикулярные основаниям, что противоречит определению пирамиды.
12.  Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?
Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?
Да (см. рисунок).
III Доказательства
I Определения, формулы
Многогранник (многогранная поверхность) — поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
Грани — многоугольники, из которых составлен многогранник.
Ребра — стороны граней многогранника.
Вершины — концы ребер многогранника.
Диагональ — отрезок, соединяющий две вершины, не принадлежащие одной грани.
Сечение — общая часть многогранника и секущей плоскости.
Призма — многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Высота призмы — перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.
Прямая призма — призма, в которой боковые ребра перпендикулярны к основаниям.
Наклонная призма — призма, в которой боковые ребра не перпендикулярны к основаниям.
Правильная призма — прямая призма, основаниями которой являются правильные многоугольники.
Площадь полной поверхности призмы: 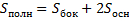
Пирамида — многогранник, составленный из n-угольника и n треугольников.
Высота пирамиды — перпендикуляр, проведенный из вершины пирамиды к плоскости основания.
Площадь полной поверхности пирамиды: 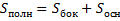
Правильная пирамида — пирамида, основанием которой является правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является высотой.
Усеченная пирамида — многогранник, гранями которого являются два n-угольника (верхнее и нижнее основания), расположенные в параллельных плоскостях, и n четырехугольников (боковых граней).
Правильная усеченная пирамида — пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию.
Правильный выпуклый многогранник — выпуклый многогранник, все грани которого являются равными правильными многоугольниками и в каждой вершине которого сходится одно и то же количество ребер.
II Вопросы
1. Какое наименьшее число ребер может иметь многогранник?
Наименьшее число ребер имеет тетраэдр — 6.
2. Призма имеет n граней. Какой многоугольник лежит в её основании?
n-угольник
3. Является ли призма прямой, если 2 её смежные боковые грани перпендикулярны к плоскости основания?
Да, является, т. к. если боковые ребра призмы перпендикулярны основанию, то призма называется прямой.
4. В какой призме боковые ребра параллельны её высоте?
В прямой призме, т. к. высота перпендикулярна основанию, так же как и боковые ребра прямой призмы перпендикулярны основанию. «Если две прямые перпендикулярны плоскости, то они параллельны».
5. Является ли призма правильной, если все её ребра равны друг другу?
Да, т. к. в правильной призме все боковые грани — равные прямоугольники —> боковые ребра равны.
6. Может ли высота одной из боковых граней наклонной призмы являться и высотой призмы?
Да, если эта грань перпендикулярна основанию призмы.
7. Существует ли призма, у которой:
а) боковое ребро перпендикулярно только одному ребру основания?
Да, в наклонной призме.
б) только одна боковая грань перпендикулярна основанию?
Нет. Если боковая грань перпендикулярна основанию, значит, призма прямая —> все боковые грани перпендикулярны основанию.
Правильная треугольная призма разбивается плоскостью, проходящей через средние линии оснований, на две призмы. Как относятся площади боковых поверхностей этих призм?
Формула площади боковой поверхности: 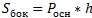 . Высоты равны —>
. Высоты равны —> 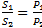 .
.  ;
; 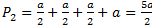 —>
—> 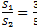 .
.
9. Будет ли пирамида правильной, если её боковыми гранями являются правильные треугольники?
Да, будет, т. к. все боковые грани правильной пирамиды — равные равнобедренные треугольники.
10. Сколько граней, перпендикулярных к плоскости основания, может иметь пирамида?
Две. Рисуем треугольник/квадрат и две грани перпендикулярные основанию.
11. Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основанию?
Нет, перпендикулярны к основанию могут быть только две смежные грани. Иначе бы через вершину пирамиды проходили бы как минимум две прямые, перпендикулярные основаниям, что противоречит определению пирамиды.
12.  Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?
Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?
Да (см. рисунок).
