Лабораторная работа №2
Среднее: типическое значение для количественных данных
| Задание 3. | Определить количество бракованных изделий в дневном выпуске. |
Каждая партия изделий компании содержит 1000 изделий. В дневном выпуске произведено 253 партии. Для проведения контроля качества изделий была случайным образом взята выборка, включающая 10 партий. Число бракованных изделий в каждой партии составило: 3, 8, 2, 5, 0, 7, 14, 7, 4, 1. Определить, какое количество бракованных изделий можно ожидать в дневном выпуске, состоящем из 253 000 изделий.
1. Откройте файл Описательная статистика.xls.
2. На Листе2 в ячейке А1 задайте метку Брак, а в диапазон A2:A11 введите исходные данные.
3. В ячейке С1 задайте метку Среднее, а в ячейке С2 вычислите Среднее (уровень брака) для бракованных изделий из заданной выборки данных.
Замечание. При расчете среднего воспользуйтесь статистической функцией СРЗНАЧ.
4. В ячейке А13 задайте метку Количество бракованных изделий. В ячейке А14 вычислите ожидаемое количество бракованных изделий в дневном выпуске.
| Задание 4. | Определить средний балл результатов обучения. |
Предположим, что в университете каждой дисциплине, в зависимости от ее важности, присваивается определенное количество очков. Система оценок включает оценки от 1,0 (незачет) до 5,0 (отлично). Студент в конце семестра имеет результаты, указанные в таблице 2. Определить средний балл студента.
Таблица 2. Оценки студента за семестр
| Дисциплина | Очки | Оценка |
| Статистика | 4,7 | |
| Экономика | 4,3 | |
| Маркетинг | 4,5 | |
| Спецкурс | 3,8 |
В данном задании элементы данных (дисциплины) нельзя рассматривать как равноценные. В этом случае целесообразно не просто усреднить оценки, а вычислить взвешенное среднее, которое позволяет учесть степень важности (вес) каждой дисциплины. Веса обычно представляют собой положительные числа, сумма которых равна 1. Формула для вычисления взвешенного среднего с учетом весов имеет следующий вид.
Взвешенное среднее = 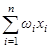
где w1, w2,…, wn – соответствующие веса, сумма которых равна 1. Для нашего примера веса определяются делением количества очков по каждой дисциплине на общее количество очков (n=15).
1. Откройте файл Описательная статистика.xls.
2. На Листе2 в ячейках F1 и G1 задайте метки Очки и Оценка соответственно. В диапазон F2:G5 введите данные Таблицы 2.
3. В ячейке F7 задайте метку Взвешенное среднее.
4. Чтобы найти взвешенное среднее, вначале дайте имена каждой колонке чисел. Для этого выделите обе колонки вместе с метками и выберите команду:
Вставка®Имя®Создать
В появившемся диалоговом окне включите опцию в строке выше и щелкните на кнопке ОК. Теперь выделите ячейку F8 и вычислите взвешенное среднее, используя из категории Полный алфавитный перечень функции Excel СУММПРОИЗВ и СУММ. Формула вычисления имеет следующий вид: =СУММПРОИЗВ(Очки;Оценка)/СУММ(Очки). Уменьшите разрядность результата до двух десятичных знаков после запятой. Вы получите средневзвешенное значение, равное 4,45.
5. Вычислите средний балл студента, просто усреднив оценки. Для этого в ячейке F10 задайте метку Среднее, а в ячейке F11 получите среднее (4,33), используя функцию СРЗНАЧ.
Как видите, результат среднего ниже средневзвешенного, т.к. не учитывает важность дисциплин. Тем не менее, низкая оценка за Спецкурс незначительно повлияла на средний балл студента, потому что вес этой дисциплины мал (всего 1 очко). Средний балл мог оказаться существенно малым, если бы студент получил низкие оценки по экономическим дисциплинам!
Таблица 3. Падение акций при открытии торгов
| Фирма | Изменение стоимости, % | Фирма | Изменение стоимости, % | Фирма | Изменение стоимости, % |
| -4,1 | -0,9 | -15,7 | |||
| -5,1 | -3,5 | -12,3 | |||
| -4,5 | -10,5 | -9,6 | |||
| -5,4 | -7,2 | -12,0 | |||
| -4,0 | -8,9 | -12,4 | |||
| -11,6 | -6,8 | -8,6 | |||
| -4,0 | -2,1 | -11,4 | |||
| -3,0 | -17,2 | -10,8 | |||
| -4,4 | -15,7 | -8,6 | |||
| -9,3 | -8,9 |
1. В файле Описательная статистика.xls на Листе3 в ячейке A1 задайте метку Изменение стоимости. В диапазон A2:A30 введите данные Таблицы 3. Увеличьте ширину столбца, дважды щелкнув на правой границе заголовка столбца A.
2. Выделите диапазон A1:A30 и выполните упорядочивание данных с помощью команды:
Данные®Сортировка…
Параметры сортировки задайте, как указано ниже на рисунке.

3. В ячейку B1 введите метку Ранг, а в ячейку B2 введите число 1. Выделите диапазон B2:B30 и выберите команду Правка®Заполнить®Прогрессия …В диалоговом окне установите опцию Шаг: равной 1 и щелкните на кнопке ОК.
4. Теперь определите значение медианы. Для этого сначала присвойте имя переменной n ячейке B30. В ячейке D1 задайте метку Ранг, а в ячейку D2 введите формулу =(n+1)/2. В ячейке D5 задайте метку Медиана.В ячейкуD6 скопируйте из столбца процентного изменения стоимости акций значение, соответствующее вычисленному рангу медианы.
5. Постройте гистограмму процентных изменений стоимости акций для диапазона данных A1:A30, включая метку. Интервал входных значений задайте явно равным 2. Нижнюю границу диапазона входных значений примите равной –20, а верхнюю границу равной 0. Значения карманов вместе с меткой Карман расположите в ячейках F1:F12. Выведите гистограмму вместе с таблицей распределения частот в область H1:Р20. Можно ли считать, что распределение данных близко к нормальному?
6. В ячейке D9 задайте метку Среднее, а в ячейке D10 рассчитайте среднее значение процентного изменения. Уменьшите разрядность полученного значения до одного знака после запятой. Существенно ли отличаются друг от друга значения среднего и медианы?
| Задание 6. | Определить медиану и среднее для служащих сферы общественного питания. |
В таблице 4 содержатся данные о количестве служащих в 10 фирмах общественного питания.
Таблица 4. Количество служащих в фирмах общественного питания
| Фирма | Количество служащих | Фирма | Количество служащих |
1. В файле Описательная статистика.xls добавьте Лист4.
2. На Листе4 в ячейке A1 задайте метку Количество служащих, а в диапазон A2:A11 введите данные из Таблицы 4.
3. Постройте гистограмму для диапазона данных A1:A11, включая метку. Интервал входных значений задайте явно равным 20000. Нижнюю границу диапазона входных значений примите равной 26000, а верхнюю границу равной 486000. Значения карманов вместе с меткой Карман расположите в ячейках D1:D25. Расположите таблицу распределения частот в диапазоне F1:G26, а гистограмму – в диапазоне I1:M20. Какой характер распределения имеют данные?
4. В ячейку J25 введите метку Медиана. В ячейке J26 вычислите медиану, используя статистическую функцию МЕДИАНА.
5. В ячейку L25 введите метку Среднее. В ячейке L26 вычислите среднее, используя статистическую функцию СРЗНАЧ. Объясните причину отличия значений медианы и среднего.
Таблица 5. Выплаты руководителям финансовых компаний
| Фирма | Зарплата и премия, дол. | Фирма | Зарплата и премия, дол. | Фирма | Зарплата и премия, дол. |
1. В файле Описательная статистика.xls добавьте Лист5.
2. На Листе5 в ячейке A1 задайте метку Выплаты, а в диапазон A2:A31 введите данные из Таблицы 5.
3. Выберите команду Сервис®Анализ данных®Ранг и персентиль и задайте параметры как указано ниже на рисунке. Щелкните на кнопке ОК.

В полученной таблице выделите столбец со значениями персентилей (диапазон F2:F31) и уменьшите разрядность до одного знака после запятой.
4. Объедините диапазон ячеек H1:N1 и введите метку Базовые показатели.
5. В ячейку H2 введите метку Наименьшее значение, а в ячейку H3 скопируйте значение из ячейки D31.
6. В ячейку K2 введите метку Наибольшее значение, а в ячейку K3 скопируйте значение из ячейки D2.
7. В ячейке N2 задайте метку Медиана. В ячейке N3, используя функцию СРЗНАЧ, вычислите медиану как среднее двух значений с рангами 15 и 16 (ячейки D16:D17).
8. В ячейках H6 и L6 задайте метки Нижний квартиль и Верхний квартиль соответственно.
9. В ячейку H7 скопируйте значение из ячейки D24, что соответствует нижнему 24,1-персентилю (это число самое близкое к 25%) с рангом 23.
10. В ячейку L7 скопируйте значение из ячейки D9, что соответствует верхнему 75,8-персентилю (это число самое близкое к 75%) с рангом 8.
11. Чтобы сделать выводы о симметричности распределения, надо сравнить три значения: медиану и квартили. Проведем визуальное сравнение. Для этого постройте для соответствующих значений (выделив ячейки N3, H7, L7) точечную диаграмму, проставьте значения точек и удалите все надписи. Вид диаграммы показан на рисунке.
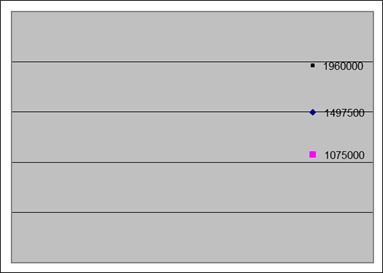
Как видим из диаграммы, значение медианы находится приблизительно посередине между квартилями, что соответствует симметричному распределению данных.
Контрольные вопросы
1. Перечислите обобщающие показатели, характеризующие типические значения набора данных.
2. Перечислите показатели, характеризующие разброс данных.
3. Перечислите и кратко опишите показатели, характеризующие степень симметричности данных.
4. Что такое среднее? Объясните среднее с точки зрения суммы всех значений набора данных.
5. Что такое взвешенное среднее? В каких случаях этот показатель используется вместо обычного среднего?
6. Что такое медиана? Как найти медиану для набора данных:
а) С четным количеством значений?
б) С нечетным количеством значений?
7. Как вычислить медиану для порядковых категорийных данных?
8. Что такое мода? В каком случае вычисляется модальный интервал?
9. Какой типический показатель (или показатели) можно использовать для:
а) Количественных данных?
б) Порядковых категорийных данных?
в) Категорийных данных, которые нельзя содержательно упорядочить?
10. Какие показатели лучше использовать:
а) При нормальном распределении данных?
б) При планировании общей суммы?
в) При ассиметричном распределении, когда общая сумма не важна?
11. Что такое персентиль? В каких единицах он выражается?
12. Что такое квартили?
13. Назовите пять базовых характеристик распределения.
Лабораторная работа №3
Таблица 1. Динамика изменения дневной прибыли на бирже
| Дата | Дневная прибыль | Дата | Дневная прибыль | Дата | Дневная прибыль |
| -0,006 | 0,009 | 0,012 | |||
| -0,004 | -0,015 | -0,004 | |||
| 0,008 | -0,006 | 0,002 | |||
| 0,011 | 0,002 | -0,008 | |||
| -0,001 | 0,011 | -0,010 | |||
| 0,017 | 0,013 | -0,013 | |||
| 0,017 | 0,002 | 0,009 | |||
| -0,004 | -0,018 | -0,020 | |||
| 0,008 | -0,014 | -0,003 | |||
| -0,002 | -0,001 | -0,001 | |||
| 0,006 | -0,001 | 0,017 | |||
| -0,017 | -0,013 | 0,001 | |||
| 0,004 | 0,030 | -0,000 | |||
| 0,015 | 0,007 | -0,035 | |||
| 0,001 | -0,007 | 0,001 | |||
| -0,005 | 0,001 | -0,014 |
5. Определите число значений дневной прибыли, находящихся в пределах одного стандартного отклонения. Сначала отфильтруйте данные, оставив значения дневной прибыли в интервале [-0,0121, 0,0114]. Для этого выделите любую ячейку в столбце A со значениями дневной прибыли и выполните команду:
Данные®Фильтр®Автофильтр
Откройте меню, щелкнув на стрелке в заголовке Дневная прибыль, и выберите (Условие…). В диалоговом окне Пользовательский автофильтр установите параметры как показано ниже. Щелкните на кнопке ОК.
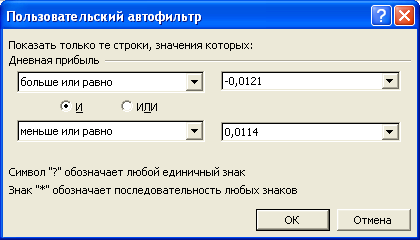
Чтобы подсчитать число отфильтрованных данных, выделите диапазон значений дневной прибыли, щелкните правой кнопкой на свободном месте в строке состояния и в контекстном меню выберите команду Количество значений. Прочтите результат. Теперь отобразите все исходные данные, выполнив команду: Данные®Фильтр®Отобразить все и выключите автофильтр с помощью команды: Данные®Фильтр®Автофильтр.
6. Вычислите процент значений дневной прибыли, удаленных от среднего на расстоянии одного стандартного отклонения. Для этого в ячейку H8 занесите метку Процент, а в ячейке H9 запрограммируйте формулу вычисления процента и получите результат с точностью до одного знака после запятой.
7. Рассчитайте интервал значений дневной прибыли в пределах двух стандартных отклонений от среднего. В ячейках D11, D12 и F12 задайте соответственно метки: Два стандартных отклонения, Нижняя граница, Верхняя граница. В ячейки D13 и F13 введите расчетные формулы и получите результат с точностью до четвертого знака после запятой.
8. Определите число значений дневной прибыли, находящихся в пределах двух стандартных отклонений, предварительно отфильтровав данные.
9. Вычислите процент значений дневной прибыли, удаленных от среднего на расстоянии двух стандартных отклонений. Для этого в ячейку H12 занесите метку Процент, а в ячейке H13 запрограммируйте формулу вычисления процента и получите результат с точностью до одного знака после запятой.
10. Рассчитайте интервал значений дневной прибыли в пределах трех стандартных отклонений от среднего. В ячейках D15, D16 и F16 задайте соответственно метки: Три стандартных отклонения, Нижняя граница, Верхняя граница. В ячейки D17 и F17 введите расчетные формулы и получите результат с точностью до четвертого знака после запятой.
11. Определите число значений дневной прибыли, находящихся в пределах трех стандартных отклонений, предварительно отфильтровав данные. Вычислите процент значений дневной прибыли. Для этого в ячейку H16 занесите метку Процент, а в ячейке H17 запрограммируйте формулу вычисления процента и получите результат с точностью до одного знака после запятой.
12. Ответьте на вопрос: можно ли считать, что «правило двух третей» выполняется, и размер дневной прибыли подчиняется нормальному распределению?
13. Постройте гистограмму дневной прибыли акций на бирже и поместите ее вместе с таблицей распределения частот в области J1:S20. Покажите на гистограмме приблизительно среднее значение и интервалы, соответствующие одному, двум и трем стандартным отклонениям от среднего соответственно.
Таблица 2. Зарплата персонала
| Код сотрудника | Зарплата, дол. | Код сотрудника | Зарплата, дол. | Код сотрудника | Зарплата, дол. |
1. Откройте файл Характеристики рассеяния.xls.
2. На Листе2 в ячейке A1 задайте метку Зарплата. В диапазон A2:A13 введите данные из Таблицы 2.
3. Отсортируйте данные по возрастанию.
4. В ячейке C1 задайте метку Размах, а в ячейке C2 запрограммируйте формулу для расчета размаха: = A13–A2.
5. В ячейке C4 задайте метку Среднее, а в ячейке C5 вычислите среднее, используя статистическую функцию СРЗНАЧ.
6. В ячейке C7 задайте метку Стандартное отклонение, а в ячейке C8 вычислите стандартное отклонение, используя статистическую функцию СТАНДОТКЛОН.
7. Постройте гистограмму зарплаты сотрудников для диапазона от 16000 (нижняя граница) до 46000 (верхняя граница), приняв значение интервала равным 5000. Значения карманов вместе с меткой Карман расположите в ячейках F1:F8. Выведите гистограмму вместе с таблицей распределения частот в область H1:P20.
Интерпретация результатов
1. Размах составляет $28000. Эта величина показывает различие между наиболее (зарплата $44500) и наименее (зарплата $16500) оплачиваемыми сотрудниками. Однако размах не отражает типичную вариацию (изменчивость) зарплаты в отделе. Для этого лучше использовать стандартное отклонение.
2. Средняя зарплата в отделе составляет $28375 и стандартное отклонение показывает, что зарплаты отдельных сотрудников отличаются от средней зарплаты приблизительно на $7459.
3. Покажите на гистограмме приблизительно величину размаха, среднее значение и стандартное отклонение.
Интерпретация результатов
Рассматриваемые два отдела различаются по уровню продаж билетов. Производительность труда при продаже театральных билетов в целом выше производительности труда при продаже билетов на симфонические концерты (средние значения составляют 35 и 23), но вместе с тем, естественно, и вариация (стандартное отклонение) в отделе продаж театральных билетов больше (7, а не 6). Однако коэффициент вариации (20%) для отдела продаж театральных билетов оказался меньше, чем коэффициент вариации (26%) для отдела продаж билетов на симфонические концерты. Это означает, что группа, работающая с театральными билетами (с точки зрения производительности отдельных сотрудников), более однородна, поскольку в ней отклонение производительности от среднего на 6% ниже (26% – 20% = 6%), чем у группы, занятой продажей билетов на симфонические концерты.
Контрольные вопросы
1. Объясните причину, приводящую к разбросу данных. Какое влияние оказывает рассеяние данных на решение экономических задач?
2. Какие характеристики используются в качестве меры рассеяния?
3. Что такое отклонение от среднего значения? Чему равно среднее значение всех отклонений?
4. Что такое дисперсия?
5. Что такое стандартное отклонение?
6. Какую из характеристик легче интерпретировать – стандартное отклонение или дисперсию? Почему?
7. Чем отличается выборочное стандартное отклонение от стандартного отклонения генеральной совокупности?
8. Поясните «правило двух третей» для нормального распределения данных.
9. Что такое размах? В каких единицах он измеряется? В каких случаях пользуются этой характеристикой?
10. Что такое коэффициент вариации? В каких единицах он измеряется?
11. Какую характеристику рассеяния лучше использовать при сравнении изменчивости в двух ситуациях при условии, что средние в этих ситуациях сильно отличаются?
Контрольные задания
Добавьте Лист4 и выполните задание с использованием базы данных служащих (файл База данных служащих.xls находится в папке Мои документы).
Замечание. Для выполнения некоторых заданий потребуется фильтрация списка, т.е. отбор из базы данных отдельных записей по условиям фильтра. В этом случае необходимо установить курсор на любой ячейке списка и включить фильтрацию с помощью команды:
Данные®Фильтр®Автофильтр
В строке заголовков таблицы появятся кнопки со стрелкой. При щелчке на стрелке соответствующего заголовка откроется меню, содержащее условия отбора. Например, если необходимо отобрать записи, содержащие данные только для мужчин, то надо щелкнуть на стрелке заголовка Пол и выбрать в меню критерий М. В результате база данных будет отфильтрована, и в списке останутся только записи, соответствующие заданному критерию (записи мужчин). Теперь нужные данные можно скопировать в другой файл и провести анализ.
После окончания анализа необходимо в файле База данных служащих.xls отменить действие фильтра. Для этого сначала выполните команду: Данные®Фильтр®Отобразить все, чтобы вывести все записи базы, а затем выключите автофильтр, повторно выполнив команду:
Данные®Фильтр®Автофильтр.
Таблица 2. Объекты недвижимости
| Объект | Объект | ||||||
| 7,8 | 26,0 | 14,6 | 37,2 | ||||
| 23,8 | 31,0 | 26,0 | 38,4 | ||||
| 28,0 | 37,4 | 30,0 | 43,6 | ||||
| 26,2 | 34,8 | 29,2 | 44,8 | ||||
| 22,4 | 39,2 | 24,2 | 40,6 | ||||
| 28,2 | 38,0 | 29,4 | 41,8 | ||||
| 25,8 | 39,6 | 23,6 | 45,2 | ||||
| 20,8 | 31,2 |
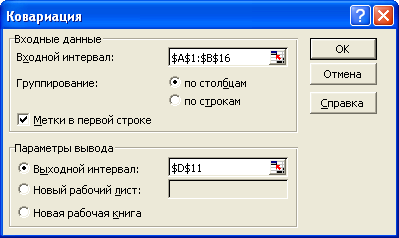 Щелкните на кнопке ОК
Щелкните на кнопке ОК
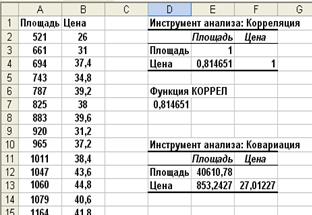 Результатом является матрица попарных ковариаций.
На диагонали расположены дисперсии для каждой переменной (квадрат стандартного отклонения).
Значение ковариации Цены и Площади (853,2427) указано в левой нижней части матрицы в ячейке E13.
Правая верхняя часть матрицы пустая, т.к. ее значения совпадают с соответствующими значениями в левой нижней части.
Результатом является матрица попарных ковариаций.
На диагонали расположены дисперсии для каждой переменной (квадрат стандартного отклонения).
Значение ковариации Цены и Площади (853,2427) указано в левой нижней части матрицы в ячейке E13.
Правая верхняя часть матрицы пустая, т.к. ее значения совпадают с соответствующими значениями в левой нижней части.
Контрольные вопросы
1. В чем отличие анализа двумерных данных от анализа одномерных данных?
2. На какие вопросы можно ответить, проанализировав двумерные данные?
3. Что такое диаграмма рассеяния? С какой целью она используется для анализа?
4. Что такое коэффициент корреляции?
5. На что указывает знак (положительный или отрицательный) коэффициента корреляции?
6. Если большие значения X вызывают появление больших значений Y, то какой, по вашему мнению, должна быть корреляция – положительной, отрицательной или нулевой? Почему?
7. Для каждого из приведенных ниже равенств укажите типичный вариант интерпретации?
а) r = 1;
б) r = 0,85;
в) r = 0;
г) r = –0,15;
д) r = –1.
8. Поясните как, по вашему мнению, располагаются точки на диаграмме рассеяния в следующих ситуациях.
а) Взаимосвязь между X и Y отсутствует.
б) Линейная взаимосвязь с сильной положительной корреляцией.
в) Линейная взаимосвязь с сильной отрицательной корреляцией.
г) Линейная взаимосвязь со слабой положительной корреляцией.
д) Линейная взаимосвязь со слабой отрицательной корреляцией.
е) Линейная взаимосвязь с корреляцией +1?
ж) Линейная взаимосвязь с корреляцией –1?
9.Что представляет собой ковариация между X и Y?
10.Какую из характеристик легче интерпретировать – корреляцию или ковариацию? Почему?
Полиномиальное приближение
Рассмотрим квадратичную модель, в которой функция регрессии представляет собой полином второй степени. Уравнение регрессии квадратичной модели имеет следующий вид.
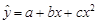
В качестве независимых переменных в уравнении используются переменные x и x2.
