Случайная величина называется равномерно распределённой на интервале [c,d], если функция плотности распределения её на этом интервале постоянна, а вне него равна нулю.
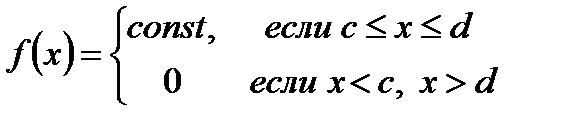
Из условия нормировки имеем: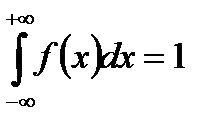 
, в нашем случае 
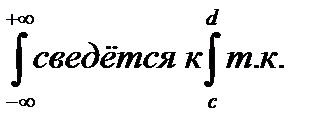за пределами этого интервала f(x)=0.
| c a b d x |
f(x)
|
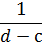
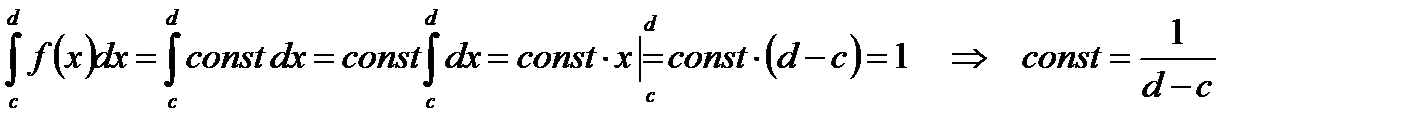
Вероятность того что X попадёт в интервал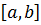 
:
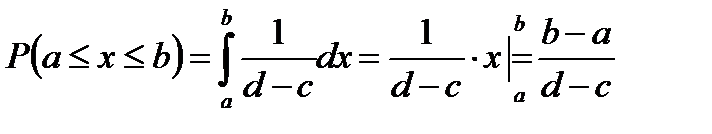
Это значит, что каждое своё значение случайная величина принимает с одинаковой вероятностью. На практике такой закон распределения встречается редко.
В реальности же с наибольшей вероятностью случайная величина принимает значения вблизи М[Х] (среднего значения), а по мере удаления от него вероятность принять такое значение уменьшается.
Нормальный закон распределения или распределение Гаусса.
Случайная величина распределена по нормальному закону, если функция плотности её распределения имеет вид:
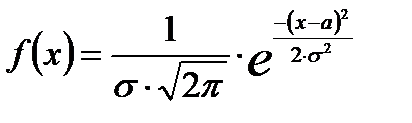где а,σ – параметры распределения.
| Pd=0,68 |
| Pd=0,954 |
| Pd=0,9972 |
|
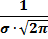
| a-3σ a-2σ a-σ a a+σ a+2σ a+3σ |
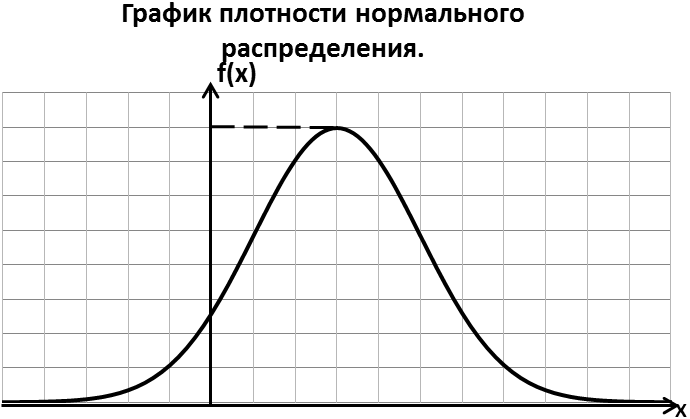
Кривая симметрична относительно прямой х=а, в этой точкеf(x) имеет максимум: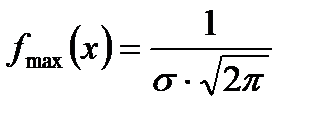 
.По условию нормировки 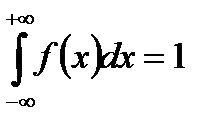площадь под кривой не меняется, но с изменением параметра а, кривая смещается по оси х:
| a3=0 |
| a2=1 |
| a1=2 |
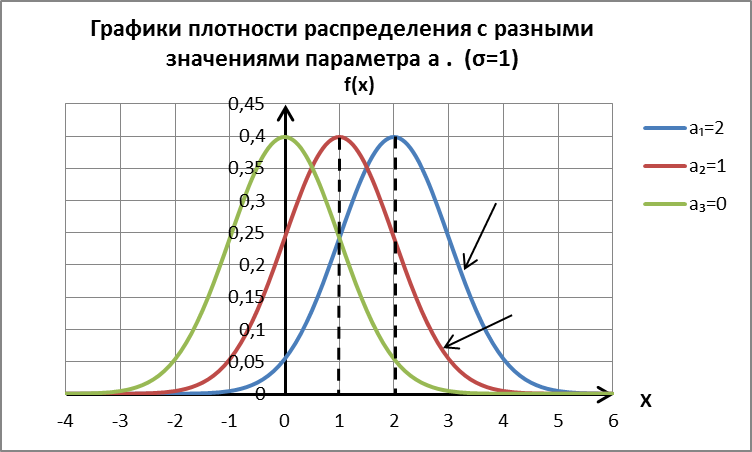
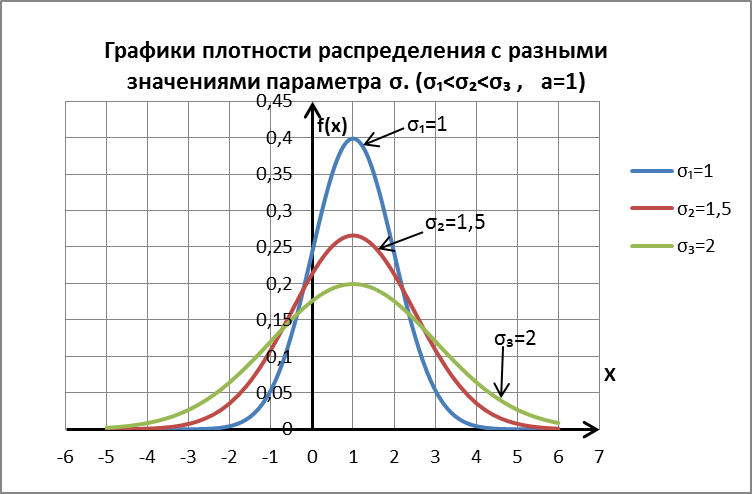
С изменением параметра σменяется форма кривой, но не площадь под ней:
|
|
|
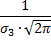
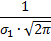
Для распределения Гаусса (нормального распределения):
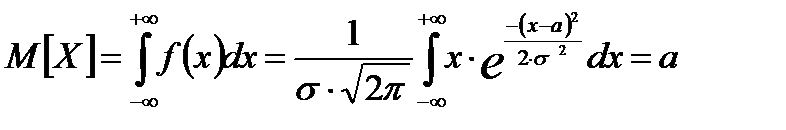
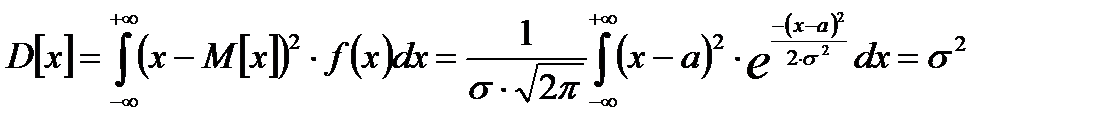
То есть, параметр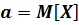 
-математическое ожидание,
параметр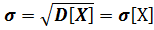 
– среднее квадратическое отклонение.
Нормальный закон распределения можно задать функцией распределения:
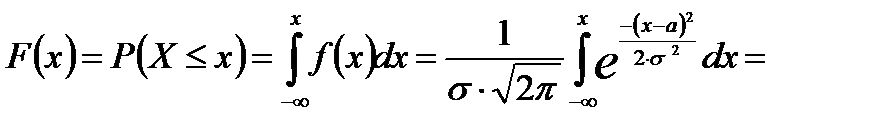
Введём замену переменной: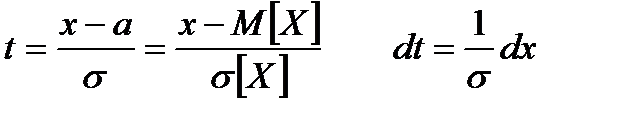 
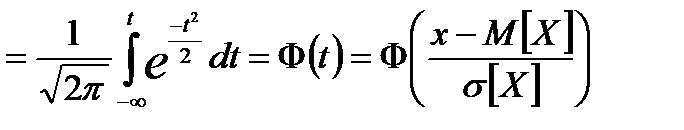
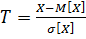это нормированная случайная величина, она – безразмерная,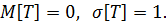 
Так как 99,7% всех значений случайной величины Х отличаются от М[Х] не больше, чем на 3·σ[Х], следовательно для любого значения x получим:
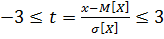с вероятностью Р=0,997.
Ф(t)– функция Гаусса или нормальная функция распределения,
Значения функции Ф(t) для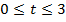 
содержатся в таблице «Нормальная функция распределения».
Свойства функции Ф(t):
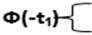
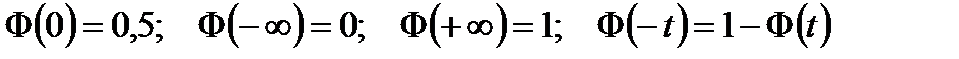
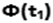
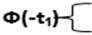
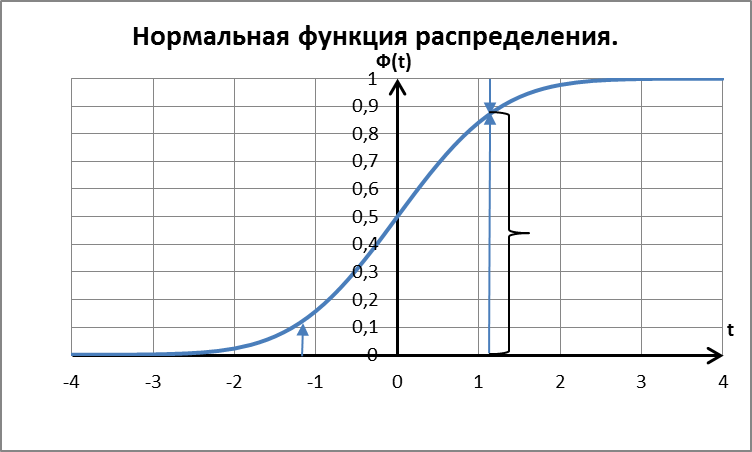
Вероятность попадания значений случайной величины в интервал [a.b]:
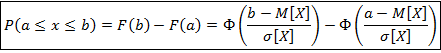
Правило трёх сигм:
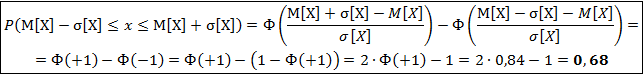
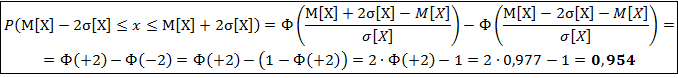
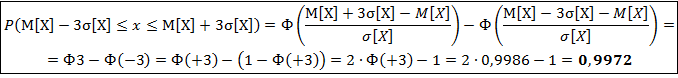
Математическая статистика.
Основные понятия математической статистики.
Математическая статистика – это раздел математики о методах регистрации, систематизации и анализа статистических экспериментальных данных, полученных в результате наблюдения массовых случайных явлений.
Статистическая совокупность – это множество объектов, обладающих общими признаками, которые являются наиболее важными (типичными) для характеристики этих объектов.
Серия измерений какого либо признака совокупности – это совокупность значений случайной величины.
Объём совокупностиn –это число членов совокупности.
Генеральная совокупность – это совокупность всех объектов, которые имеют типичную характеристику или признак. Это все возможные значения случайной величины. Объём генеральной совокупности (n →∞).
Изучить всю генеральную совокупность практически невозможно, поэтому изучают её часть – выборочную совокупность.
Выборочная совокупность (выборка) – это отобранная тем или иным способом часть генеральной совокупности (n конечно).
Из одной генеральной совокупности можно отбирать сколь угодно много выборок, главное, чтобы выборка была репрезентативной (представительной), а для этого элементы выборки должны отбираться случайным образом.
Пример: признак - рост мужчины в России.
Генеральная совокупность -- все мужчины в стране.
Выборка -- случайно отобранные мужчины из разных регионов страны (не в секции баскетбола).
Варианта – это числовое значение изучаемого признака( отдельные значения случайной величины).
Основные задачи, которые стоят перед математической статистикой:
1. Определение закона распределения случайной величины по имеющимся статистическим данным ( по выборке – закон распределения для всей генеральной совокупности).
2. Определение неизвестных параметров распределения ( по выборке оценить параметры генеральной совокупности).
3. Задача проверки правдоподобия выдвигаемых статистических гипотез.
1. Схема предварительной обработки экспериментальных данных.
1). Сбор экспериментальных данных.
Чтобы определить закон распределения случайной величины, то есть связь между значениями случайной величины (вариантами) и вероятностями , с которыми случайная величина эти значения принимает, нужно провести серию измерений или подсчётов для интересующей нас случайной величины (признака).
В результате получаем статистический ряд – это совокупность числовых данных или выборка объёмом n:
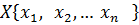
Затем производят упорядочивание членов выборки – эта операция называется ранжирование.
Ранжирование -- это расположение всех имеющихся вариант по возрастанию. Получаем ранжированный статистический ряд.
Пример: при измерении частоты пульса у 10 пациентов получены следующие результаты: 90, 110, 65, 80, 90, 60, 70, 80, 70, 80
Ранжированный ряд имеет вид: 60, 65, 70, 70, 80, 80, 80, 90, 90, 110.
Колебания изучаемого признака называются варьирование, В нашем примере варьирование - это изменение частоты пульса.