Анализируя диаграммы рассеяния двумерной совокупности данных, можно выявить три различных типа взаимосвязей между переменными X и Y.
1. Линейная взаимосвязь.
2. Отсутствие взаимосвязи.
3. Нелинейная взаимосвязь.
Линейная взаимосвязь играет такую же важную роль для двумерных данных, как и нормальное распределение для одномерных данных.
Прежде всего, линейную зависимость между переменными X и Y легче анализировать.
На диаграмме рассеяния точки случайным образом могут концентрироваться вокруг прямой линии, или быть достаточно широко разбросаны, образуя некоторое облако.
Набор данных линейной взаимосвязи не должен содержать сильных выбросов.
Отсутствие взаимосвязи представляет собой особый случай линейной взаимосвязи, когда соответствующая диаграмма рассеяния имеет совершенно случайный характер, т. е. продвигаясь по ней слева направо, мы не обнаруживаем тенденции направленности вверх (увеличение) или вниз (уменьшение).
Такая диаграмма имеет вид либо круглого, либо овального облака.
Овал может иметь вертикальную или горизонтальную ориентацию, но без наклона.
Фактически, если совокупность данных характеризуется отсутствием взаимосвязи, то, изменяя шкалу той или другой переменной, можно добиться того, что диаграмма рассеяния будет иметь круговую или овальную форму разброса точек.
Нелинейная взаимосвязь характеризуется тем, что в двумерной совокупности данных точки на диаграмме рассеяния группируются вокруг некоторой кривой линии.
Поскольку разновидностей кривых может быть чрезвычайно много, анализ нелинейной взаимосвязи существенно сложнее, чем линейной.
Для переменных X и Y с нелинейной зависимостью корреляционный и регрессионный анализ следует использовать с осторожностью.
В некоторых задачах бывает полезно преобразовать одну или обе переменные таким образом, чтобы получить между ними линейную взаимосвязь.
Это позволяет упростить анализ (применив корреляцию и регрессию к линейной взаимосвязи), а полученные результаты, если удается, преобразовывают обратно в исходную форму.
Важным шагом при выборе нелинейной формы зависимости является изучение графика.
Ниже на рисунке изображены четыре выпуклые нелинейные кривые, которые могут быть получены на графике.
Метка для каждой кривой обозначает направление выпуклости.
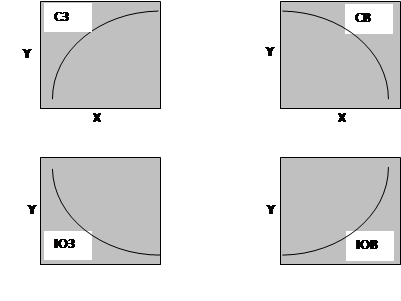
Направление выпуклости соответствует определенному виду функции регрессии. Так, для данных, имеющих выпуклость в сторону северо-запада (СЗ), используются степенные (при x>1) и логарифмические функции; для данных, имеющих выпуклость в сторону юго-запада (ЮЗ), используются степенные, логарифмические или экспоненциальные функции; данным с выпуклостью в сторону юго-востока (ЮВ) соответствуют степенные (при x>1) и экспоненциальные функции. Кроме того, все четыре кривые данных могут быть смоделированы квадратичной функцией (полиномом второй степени). Если вид данных на графике не подходит к указанным выше примерам, то следует использовать какую-либо другую форму зависимости. Например, если данные имеют две выпуклости (S-форма), то можно применить кубическую функцию (полином третьей степени). В данной лабораторной работе рассмотрим четыре модели нелинейной зависимости между двумя переменными X и Y: полиномиальную, логарифмическую, степенную и экспоненциальную. В качестве примера используем данные о ценах объектов недвижимости (см. лабораторную работу №5, таблицу 1). Зависимой переменной Y является стоимость в тысячах долларов, а независимой переменной X – площадь в квадратных метрах. Из проведенного в лабораторной работе №6 линейного регрессионного анализа для указанных данных получены график линейной функции регрессии и график остатков. На графике остатков видно, что первые два объекта недвижимости с небольшой площадью и последние несколько объектов с большой площадью имеют отрицательные остатки. Это наблюдение показывает, что нелинейное приближение может дать лучшие результаты. При внимательном рассмотрении диаграммы рассеяния (см. лабораторную работу №5, задание 1) можно заметить, что график функции регрессии имеет небольшую выпуклость в сторону СЗ, хотя кривизна небольшая. Следовательно, для анализа можно использовать квадратичную, степенную или логарифмическую функции. |
Полиномиальное приближение
Рассмотрим квадратичную модель, в которой функция регрессии представляет собой полином второй степени. Уравнение регрессии квадратичной модели имеет следующий вид.
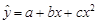
В качестве независимых переменных в уравнении используются переменные x и x2.
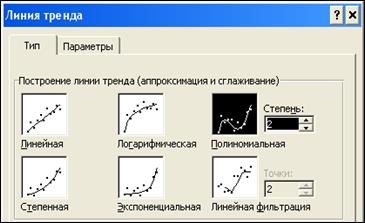 16. В диалоговом окне на вкладке Тип щелкните по пиктограмме Полиномиальная. Параметр Степень: должен соответствовать числу 2.
17. Откройте вкладку Параметры и
18. в области Название аппроксимирующей (сглаженной) кривой выберите опцию автоматическое:.
19. Убедитесь, что опция пересечение кривой с осью Y в точке: не отмечена.
20. Включите опции показывать уравнение на диаграмме и
21. поместить на диаграмму величину достоверности аппроксимации (R^2).
22. Щелкните на кнопке ОК.
23. Выделите текст с уравнением регрессии и значением R2, щелкните у его границы и расположите под заголовком диаграммы.
Результат приближения квадратичной функцией немного лучше, чем при линейном приближении, т.к. коэффициент детерминации R2, равный 68%, получился больше 66%.
Для более точного анализа квадратичной модели получим дополнительные характеристики регрессии, используя инструмент анализа Регрессия.
24. Скопируйте данные с Листа1 (диапазон A1:B16) на Лист2 в такой же диапазон.
25. Выделите столбец B и
26. из контекстного меню выберите команду Добавить ячейки.
27. В ячейку B1 введите метку Площадь^2.
28. Увеличьте ширину столбца B, дважды щелкнув на правой границе его заголовка.
29. Выделите ячейку B2 и введите в нее формулу =A2^2.
30. Скопируйте формулу в остальные ячейки столбца B, выделив ячейку B2 и
31. дважды щелкнув по маркеру заполнения.
32. Выберите команду: Сервис®Анализ данных®Регрессия.
33. В диалоговом окне Регрессия установите параметры как указано ниже на рисунке.
34. Щелкните на кнопке ОК.
16. В диалоговом окне на вкладке Тип щелкните по пиктограмме Полиномиальная. Параметр Степень: должен соответствовать числу 2.
17. Откройте вкладку Параметры и
18. в области Название аппроксимирующей (сглаженной) кривой выберите опцию автоматическое:.
19. Убедитесь, что опция пересечение кривой с осью Y в точке: не отмечена.
20. Включите опции показывать уравнение на диаграмме и
21. поместить на диаграмму величину достоверности аппроксимации (R^2).
22. Щелкните на кнопке ОК.
23. Выделите текст с уравнением регрессии и значением R2, щелкните у его границы и расположите под заголовком диаграммы.
Результат приближения квадратичной функцией немного лучше, чем при линейном приближении, т.к. коэффициент детерминации R2, равный 68%, получился больше 66%.
Для более точного анализа квадратичной модели получим дополнительные характеристики регрессии, используя инструмент анализа Регрессия.
24. Скопируйте данные с Листа1 (диапазон A1:B16) на Лист2 в такой же диапазон.
25. Выделите столбец B и
26. из контекстного меню выберите команду Добавить ячейки.
27. В ячейку B1 введите метку Площадь^2.
28. Увеличьте ширину столбца B, дважды щелкнув на правой границе его заголовка.
29. Выделите ячейку B2 и введите в нее формулу =A2^2.
30. Скопируйте формулу в остальные ячейки столбца B, выделив ячейку B2 и
31. дважды щелкнув по маркеру заполнения.
32. Выберите команду: Сервис®Анализ данных®Регрессия.
33. В диалоговом окне Регрессия установите параметры как указано ниже на рисунке.
34. Щелкните на кнопке ОК.
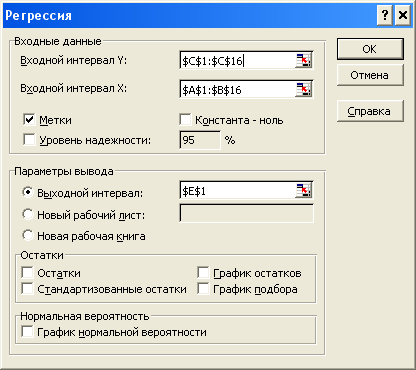 35. Выделите диапазон столбцов E:M и увеличьте ширину столбцов,
36. дважды щелкнув по правой границе в строке заголовков столбцов.
37. Удалите часть результатов, относящихся к дисперсионному анализу.
38. Для этого выделите диапазон E10:M14 и
39. выберите из контекстного меню команду Удалить…
40. В диалоговом окне установите опцию ячейки, со сдвигом вверх.
41. Щелкните на кнопке ОК.
35. Выделите диапазон столбцов E:M и увеличьте ширину столбцов,
36. дважды щелкнув по правой границе в строке заголовков столбцов.
37. Удалите часть результатов, относящихся к дисперсионному анализу.
38. Для этого выделите диапазон E10:M14 и
39. выберите из контекстного меню команду Удалить…
40. В диалоговом окне установите опцию ячейки, со сдвигом вверх.
41. Щелкните на кнопке ОК.
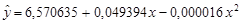 .
В линейной модели (см. лабораторную работу №6) мы получили стандартную ошибку и нормированный коэффициент детерминации равными $3238 и 0,6377 соответственно.
По сравнению с линейной моделью данная квадратичная модель имеет немного большую стандартную ошибку ($3266) и меньшее значение нормированного коэффициента детерминации (0,6315).
Исходя из этого, можно сказать, что квадратичная модель не является лучше линейной.
.
В линейной модели (см. лабораторную работу №6) мы получили стандартную ошибку и нормированный коэффициент детерминации равными $3238 и 0,6377 соответственно.
По сравнению с линейной моделью данная квадратичная модель имеет немного большую стандартную ошибку ($3266) и меньшее значение нормированного коэффициента детерминации (0,6315).
Исходя из этого, можно сказать, что квадратичная модель не является лучше линейной.
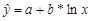 .
В качестве независимой переменной в уравнении используется
.
В качестве независимой переменной в уравнении используется 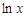 .
Так как при построении линии тренда Excel проводит логарифмирование, то значения переменной X должны быть положительными. Если же среди значений переменной X имеются нулевые или отрицательные значения, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Логарифмическая будет выделена серым цветом.
.
Так как при построении линии тренда Excel проводит логарифмирование, то значения переменной X должны быть положительными. Если же среди значений переменной X имеются нулевые или отрицательные значения, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Логарифмическая будет выделена серым цветом.
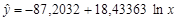 .
По сравнению с линейной моделью данная логарифмическая модель имеет меньшую стандартную ошибку ($3108<3238) и большее значение нормированного коэффициента детерминации (0,6662>0,6377). Следовательно, логарифмическая модель является несколько лучше линейной.
.
По сравнению с линейной моделью данная логарифмическая модель имеет меньшую стандартную ошибку ($3108<3238) и большее значение нормированного коэффициента детерминации (0,6662>0,6377). Следовательно, логарифмическая модель является несколько лучше линейной.
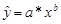 .
При построении линии тренда Excel сначала преобразует степенную модель в линейную. Для этого проводится логарифмирование обеих частей уравнения:
.
При построении линии тренда Excel сначала преобразует степенную модель в линейную. Для этого проводится логарифмирование обеих частей уравнения:
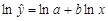 .
Затем применяется обычная линейная регрессия для зависимой переменной
.
Затем применяется обычная линейная регрессия для зависимой переменной 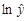 и независимой переменной
и независимой переменной 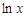 .
В результате Excel определит коэффициент регрессии, соответствующий коэффициенту b степенной модели, и постоянный член
.
В результате Excel определит коэффициент регрессии, соответствующий коэффициенту b степенной модели, и постоянный член 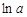 . Чтобы получить уравнение регрессии степенной модели, необходимо определить коэффициент a. Для этого выполняется обратное преобразование, т.е. коэффициент a вычисляется по формуле:
. Чтобы получить уравнение регрессии степенной модели, необходимо определить коэффициент a. Для этого выполняется обратное преобразование, т.е. коэффициент a вычисляется по формуле: 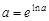 .
Поскольку Excel выполняет логарифмическое преобразование исходных данных X и Y, то, как зависимая переменная Y, так и независимая переменная X должны быть положительными. Если какое-либо из значений X или Y равно нулю или отрицательно, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Степенная будет выделена серым цветом.
.
Поскольку Excel выполняет логарифмическое преобразование исходных данных X и Y, то, как зависимая переменная Y, так и независимая переменная X должны быть положительными. Если какое-либо из значений X или Y равно нулю или отрицательно, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Степенная будет выделена серым цветом.
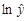 , а независимой –
, а независимой – 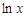 . Эти результаты нельзя сравнивать с линейной моделью, рассмотренной в лабораторной работе №6, так как стандартная ошибка в этом случае определяется в единицах измерения
. Эти результаты нельзя сравнивать с линейной моделью, рассмотренной в лабораторной работе №6, так как стандартная ошибка в этом случае определяется в единицах измерения 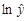 , а значение нормированного коэффициента детерминации является долей изменений
, а значение нормированного коэффициента детерминации является долей изменений 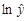 , выраженной через
, выраженной через 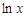 . Для получения уравнения степенной модели необходимо вычислить коэффициент a, выполнив обратное преобразование.
. Для получения уравнения степенной модели необходимо вычислить коэффициент a, выполнив обратное преобразование.
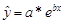 .
При построении линии тренда Excel сначала преобразует экспоненциальную модель в линейную. Для этого проводится логарифмирование обеих частей уравнения:
.
При построении линии тренда Excel сначала преобразует экспоненциальную модель в линейную. Для этого проводится логарифмирование обеих частей уравнения:
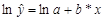 .
Затем применяется обычная линейная регрессия для зависимой переменной
.
Затем применяется обычная линейная регрессия для зависимой переменной 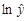 и независимой переменной х. В результате Excel определит коэффициент регрессии, соответствующий коэффициенту b экспоненциальной модели, и постоянный член
и независимой переменной х. В результате Excel определит коэффициент регрессии, соответствующий коэффициенту b экспоненциальной модели, и постоянный член 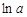 . Чтобы получить уравнение регрессии экспоненциальной модели, необходимо определить коэффициент a. Для этого выполняется обратное преобразование, т.е. коэффициент a вычисляется по формуле:
. Чтобы получить уравнение регрессии экспоненциальной модели, необходимо определить коэффициент a. Для этого выполняется обратное преобразование, т.е. коэффициент a вычисляется по формуле: 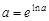 .
Поскольку Excel выполняет логарифмическое преобразование исходных данных Y, то значения зависимой переменная Y должны быть положительными. Если какое-либо из значений Y равно нулю или отрицательно, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Экспоненциальная будет выделена серым цветом.
.
Поскольку Excel выполняет логарифмическое преобразование исходных данных Y, то значения зависимой переменная Y должны быть положительными. Если какое-либо из значений Y равно нулю или отрицательно, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Экспоненциальная будет выделена серым цветом.
| Год | Продажи |
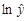 , а независимой – х. Эти результаты нельзя сравнивать с линейной моделью, рассмотренной в лабораторной работе №6, так как стандартная ошибка в этом случае определяется в единицах измерения
, а независимой – х. Эти результаты нельзя сравнивать с линейной моделью, рассмотренной в лабораторной работе №6, так как стандартная ошибка в этом случае определяется в единицах измерения 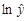 , а значение нормированного коэффициента детерминации является долей изменений
, а значение нормированного коэффициента детерминации является долей изменений 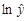 . Для получения уравнения экспоненциальной модели необходимо вычислить коэффициент a, выполнив обратное преобразование.
. Для получения уравнения экспоненциальной модели необходимо вычислить коэффициент a, выполнив обратное преобразование.
Контрольные вопросы
22. Какие типы взаимосвязей существуют между переменными X и Y? Как можно определить взаимосвязь по диаграмме рассеяния?
23. Как определяется форма нелинейной взаимосвязи с помощью графика?
24. Какие характеристики используются при сравнении нелинейной регрессионной модели с линейной регрессией?
25. Как по найденной регрессионной модели осуществляется прогнозирование переменной Y?
26. Какой вид имеет квадратичная модель регрессии? Какие переменные в уравнении используются в качестве независимых?
27. Какой вид имеет логарифмическая модель регрессии? Какая переменная в уравнении регрессии является независимой? Какое ограничение имеют значения переменной X в логарифмической модели?
28. Какой вид имеет степенная модель регрессии? С какой целью в Excel проводится логарифмическое преобразование уравнения регрессии? Что такое обратное преобразование?
29. Какой вид имеет экспоненциальная модель регрессии? Как определяются коэффициенты a и b уравнения регрессии?
