Согласно тому что функция, непрерывна в замкнутом интервале и принимающая на концах этого интервала значения разных знаков, хотя бы один раз обращается в нудь внутри интервала.
Пусть функция 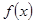 непрерывна на отрезке [
непрерывна на отрезке [ 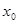 ,
, 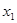 ]. Процедура метода заключается в последовательном сокращении длинны отрезка для локализации корня уравнения. Первоначально проверяются значения заданной функции на концах отрезка.
]. Процедура метода заключается в последовательном сокращении длинны отрезка для локализации корня уравнения. Первоначально проверяются значения заданной функции на концах отрезка.
В случае, если
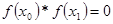 ,
,
Один из концов отрезка является корнем уравнения.
Пусть на концах отрезка значения функции имеют разные знаки, то есть имеет место соотношение 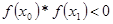 ,
,
Вычисляется значение аргумента в середине отрезка, 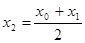 , и вычисляется значение
, и вычисляется значение
функции 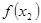 в этой точке.
в этой точке.
Далее сравниваются знаки функций в точке 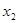 например, в левой точке
например, в левой точке 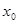 отрезка.
отрезка.
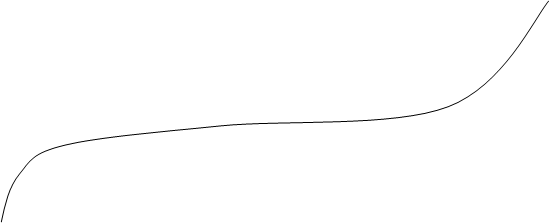
Если имеет место соотношение 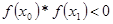 (рис.3.1), то корень следует искать на отрезке
(рис.3.1), то корень следует искать на отрезке 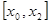 . В противном случае-корень разыскивается на отрезке
. В противном случае-корень разыскивается на отрезке 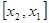 , в результате выполненной операции исходный отрезок сократился вдвое.
, в результате выполненной операции исходный отрезок сократился вдвое.
 | |||
 | |||
| |
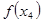
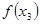
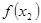
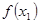
 | |||||||
 | |||||||
 | |||||||
 |
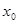
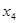
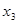
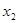
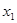
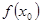
Схема метода половинного деления.
Далее, в зависимости от ситуации, отрезок вновь делится пополам,

И так далее.
Для прекращения вычислительной процедуры применяют различные критерии:
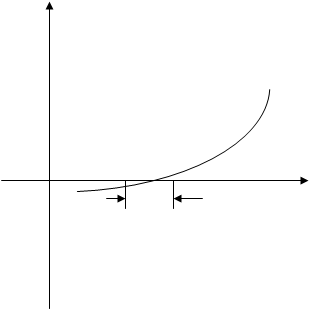
-если функция достаточно ‘пологая’, имеет смысл использовать условие (рис. а).
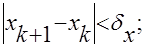
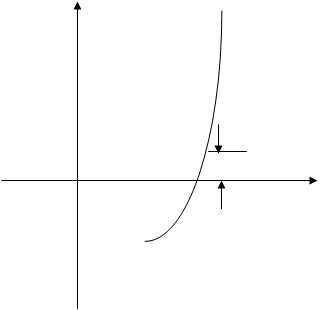
-если функция ‘круто’ меняет своё значение, целесообразно применять условие(рис. b).
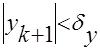
|
 |  |
|
Частные случаи поиска корня нелинейного уравнения
В случае, если заранее неизвестен характер ‘поведения’ функции, имеет смысл использовать одновременно оба условия для прекращения итерационного процесса.
Лабораторная работа № 5
Решение нелинейных уравнений.
Цель работы:
1. Получение практических навыков в организации итерационных циклов.
2. Знакомство с методами решения алгебраических и трансцендентных уравнений.
3. Получение навыков составления блок-схемы алгоритма и определения данных.
Постановка задачи:
1. Для конкретного варианта найти корень уравнения F(x) = 0 с точностью e=10-4, используя один из численных методов. На печать вывести вычисленное значение корня и для сравнения точное значение корня.
2. Значения a, b, x0, e вводятся с клавиатуры. Должен быть предусмотрен контроль вводимых значений.
3. В программе необходимо предусмотреть подсчет и вывод на печать числа итераций, за которое удается найти значение корня с заданной точностью.
Содержание отчета :
1. Постановка задачи для конкретного варианта и исходные данные.
2. Описание и блок-схема метода решения.
3. Текст программы.
Распечатка результатов работы программы в следующем виде:
РЕШЕНИЕ УРАВНЕНИЯ
ТОЧНОЕ ЗНАЧЕНИЕ КОРНЯ .............................
ВЫЧИСЛЕННОЕ ЗНАЧЕНИЕ КОРНЯ .............….
ЧИСЛО ИТЕРАЦИЙ ...........................................
Образец выполнения задания.
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом итераций.
Постановка задачи для конкретного варианта и исходные данные:
1. Найти корень уравнения : 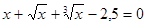 с точностью e=10-4, корень уравнения находится на отрезке (0.4, 1), используя метод итераций. На печать вывести вычисленное значение корня и для сравнения точное значение корня, точное значение корня x=0.7376.
с точностью e=10-4, корень уравнения находится на отрезке (0.4, 1), используя метод итераций. На печать вывести вычисленное значение корня и для сравнения точное значение корня, точное значение корня x=0.7376.
Значения :
Xо – примерное значение корня,
e - точность нахождения корня, вводятся с клавиатуры.
Должен быть предусмотрен контроль вводимых значений.
2. В программе необходимо предусмотреть подсчет и вывод на печать числа итераций, за которое удается найти значение корня с заданной точностью.
Описание и блок-схема метода решения:
Описание метода итераций:
Пусть уравнение 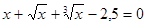 имеет один корень на отрезке [a;b]. Функция F(x) непрерывна на отрезке [a; b].
имеет один корень на отрезке [a;b]. Функция F(x) непрерывна на отрезке [a; b].
Этот метод заключается в замене уравнения 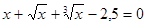 эквивалентным ему уравнением вида
эквивалентным ему уравнением вида 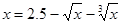
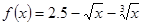
После этого строится итерационный процесс:
На заданном отрезке [a; b] выберем точку х0 – нулевое приближение – и найдем:
х1 = f(x0),
потом найдем:
х2 = f(x1),
и т.д.
Таким образом, процесс нахождения корня уравнения сводится к последовательному вычислению чисел:
хn = f(xn-1) n = 1,2,3..... .
Процесс итераций продолжается до тех пор, пока 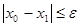
где e – заданная абсолютная погрешность корня х.
Блок-схема метода итераций:
 | |||
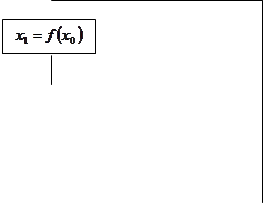 |
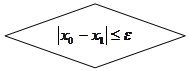 true false
true false
 | |||||
 | 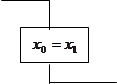 | ||||
Текст программы.
program lab5{ вариант № 3};
uses crt;
var x0,x1,a,b,e:real;
iteraz:integer;
function fun(x:real):real;
begin
fun:=2.5-sqrt(x)-exp((1/3)*(ln(x)));
end;
begin
clrscr;
write('Введите приближённое значение X=');
readln(x1);
write('Введите точность e=');
readln(e);
iteraz:=0;
repeat
iteraz:=iteraz+1;
x0:=x1;
x1:=fun(x0);
until (abs(x1-x0)<=e);
writeln('Решение уравнения:');
writeln('Точное значение корня...... ……0.7376');
writeln('Вычисленное значение корня…',x1:6:5);
writeln('Число итераций..…………......... ',iteraz);
writeln('Программа закончена, нажмите Enter.');
readln;
end.
Распечатка результатов работы программы в следующем виде:
| Решение уравнения: Точное значение корня...... ……...0.7376 Вычисленное значение корня.. …0.73767 Число итераций...........………….. ..989 |
Лабораторная работа № 5, вариант № 3.

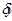 b
b
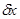 а
а