Одним из наиболее простых методов решения задачи безусловной оптимизации является метод Ньютона. Для этого целевую функцию дифференцируют в частных производных и приравнивают эти производные к нулю.
Пусть имеется зависимость
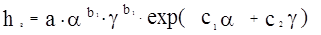 .
.
Найти такие значения a и g , при которых hз = min. Дифференцируя в частных производных, получим
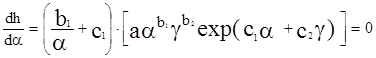 ;
;
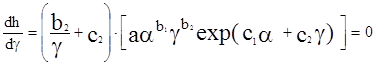 .
.
Так как 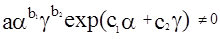 , то
, то 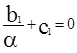 ;
; 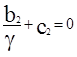 .
.
Отсюда 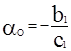 ;
; 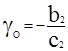 .
.
Другим методом решения задачи безусловной оптимизации является покоординатный метод.
Покоординатный метод определения максимума функции нескольких переменных в области [z 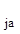 , z
, z 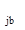 ] включает в себя многократное решение (поочередно для каждой переменной) задачи определения максимума функции одной переменной.
] включает в себя многократное решение (поочередно для каждой переменной) задачи определения максимума функции одной переменной.
Максимум функции одной переменной определяется методом золотого сечения. Для этого в области [z 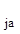 , z
, z 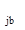 ], на которой решается задача оптимизации, задается начальная точка z
], на которой решается задача оптимизации, задается начальная точка z 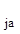 , а целевая функция рассматривается при фиксированных значениях всех факторов кроме одного, изменяющегося в пределах
, а целевая функция рассматривается при фиксированных значениях всех факторов кроме одного, изменяющегося в пределах
z 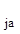
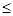 z
z 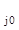
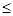 z
z 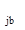 .
.
Устанавливают два значения этого фактора, равные
z 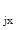 = 0,618 z
= 0,618 z 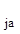 + 0,382 z
+ 0,382 z 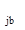 ;
;
z 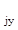 = 0,382 z
= 0,382 z 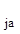 + 0,618 z
+ 0,618 z 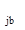 .
.
Затем вычисляют соответствующие им значения целевой функции
R 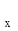 = F(z
= F(z 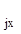 ) и R
) и R 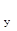 = F(z
= F(z 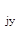 )
)
и сравнивают их между собой.
Если R 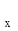 > R
> R 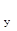 , то z
, то z 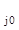 < z
< z 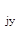 . Тогда оптимум фактора z
. Тогда оптимум фактора z 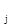 должен лежать в пределах z
должен лежать в пределах z 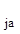
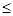 z
z 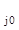
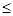 z
z 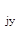 , а z
, а z 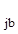 присваивается значение, равное
присваивается значение, равное
z 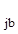 = z
= z 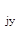 ,
,
Если R 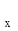 < R
< R 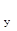 , то z
, то z 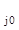 > z
> z 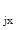 . Тогда оптимум фактора z
. Тогда оптимум фактора z 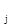 должен лежать в пределах
должен лежать в пределах
z 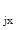
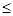 z
z 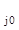
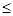 z
z 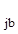 ,
,
а z 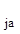 присваивается значение, равное
присваивается значение, равное
z 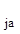 = z
= z 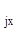 .
.
Сужение пределов осуществляется последовательно до тех пор, пока разность верхней и нижней границ не будет превышать точности вычислений.
Оптимум фактора z 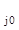 определяется как полусумма верхней и нижней границ
определяется как полусумма верхней и нижней границ
z 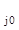 = (z
= (z 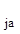 + z
+ z 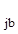 ) / 2 .
) / 2 .
Это значение принимают за начальное при определении оптимума следующего фактора z 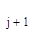 .
.
В результате каждого шага начальная точка перемещается ближе к оптимуму. Этот процесс продолжается до тех пор, пока разность между начальной и конечной точками не будет меньше точности вычислений.
|

Нелинейное программирование
Задача определения экстремума нелинейной целевой функции
F 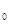 ( z
( z 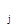 ) = extr , j = 1 . . . n
) = extr , j = 1 . . . n
при нелинейных ограничениях - равенствах
F 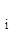 (z
(z 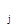 ) - R
) - R 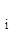 = 0 , i = 1 . . . m
= 0 , i = 1 . . . m
решается методом множителей Лагранжа.
Для решения этой задачи составляют вспомогательную функцию n переменных z 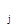 и m неопределенных множителей
и m неопределенных множителей 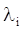 (функцию Лагранжа)
(функцию Лагранжа)
Ф (z 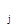 ,
, 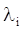 ) = F
) = F 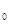 ( z
( z 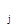 ) +
) + 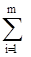
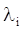 [F
[F 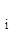 ( z
( z 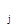 ) - R
) - R 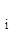 ]
]
и решают систему n + m уравнений:
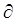 Ф (z
Ф (z 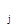 ,
, 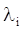 ) /
) / 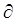 z
z 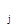 = 0 ;
= 0 ;
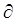 Ф (z
Ф (z 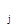 ,
, 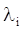 ) /
) / 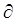
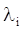 = 0 .
= 0 .
8.6. Линейное программирование
Сформулированную Л. В. Канторовичем задачу линейного программирования определения таких значений переменных z 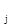 , которые в условиях заданных линейных ограничений на параметры R
, которые в условиях заданных линейных ограничений на параметры R 
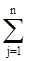 a
a 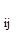 z
z 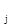
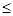 [R
[R  ]
]
обеспечивают максимум линейной целевой функции
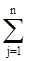 a
a 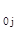 z
z 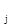 = max ,
= max ,
решают симплекс-методом, разработанным Дж. Данцигом.
Систему линейных ограничений-неравенств заменяют системой линейных ограничений-равенств путем введения дополнительных переменныхy  . При этом свободный член целевой функции полагают равным нулю
. При этом свободный член целевой функции полагают равным нулю
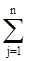 a
a 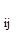 z
z 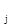 + y
+ y  = b
= b  ;
;
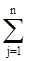 a
a 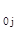 z
z 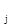 + y
+ y 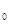 = 0 .
= 0 .
Систему уравнений приводят к виду
y  = b
= b  - [
- [ 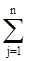 a
a 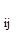 z
z 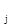 ] ;
] ;
y 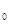 = 0 - [
= 0 - [ 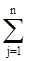 a
a 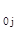 z
z 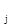 ] .
] .
Полученную систему уравнений представляют в виде таблицы, включающей в себя матрицу из коэффициентов и свободных членов ограничений и целевой функции:
z 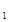
| . . . | z 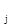
| . . . | z 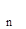
| ||
y 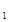
| b 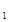
| a 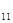
| . . . | a 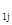
| . . . | a 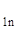
|
| . . . | . . . | . . . | . . . | . . . | . . . | . . . |
y 
| b 
| a 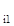
| . . . | a 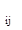
| . . . | a 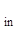
|
| . . . | . . . | . . . | . . . | . . . | . . . | . . . |
y 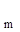
| b 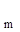
| a 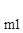
| . . . | a 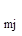
| . . . | a 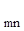
|
y 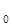
| b 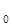
| a 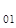
| a 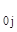
| a 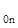
|
Если положить все основные переменные z 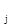 , равными нулю,
, равными нулю,
то y  = b
= b  . Это решение можно принять за базисное решение. Однако это решение еще не оптимально.
. Это решение можно принять за базисное решение. Однако это решение еще не оптимально.
Для нахождения оптимального решения необходимо поменять местами основные переменные z 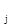 с равным количеством дополнительных переменных y
с равным количеством дополнительных переменных y  , т.е. перевести дополнительные переменные y
, т.е. перевести дополнительные переменные y  в базис, равные нулю. Для этого поочередно в каждом столбце коэффициентов определяют разрешающий элементa
в базис, равные нулю. Для этого поочередно в каждом столбце коэффициентов определяют разрешающий элементa 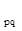 , т.е. положительный элемент столбца, имеющий максимальное отношение к абсолютной величине свободного члена
, т.е. положительный элемент столбца, имеющий максимальное отношение к абсолютной величине свободного члена
a 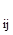 / |b
/ |b  | = max .
| = max .
Разрешающий элемент заменяют на обратную величину
a 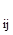 = 1 / a
= 1 / a 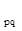 .
.
Все остальные элементы разрешающей строки делят на разрешающий элемент
b  = b
= b 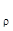 / a
/ a 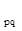 ;a
;a 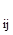 = a
= a 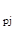 / a
/ a 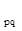 .
.
Все остальные элементы разрешающего столбца делят на разрешающий элемент и меняют знак на обратный
a 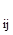 = - a
= - a 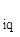 / a
/ a 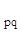 .
.
Из каждого из оставшихся элементов вычитают произведение элемента разрешающего столбца из той же строки и элемента из разрешающей строки из того же столбца, деленное на разрешающий элемент
b  = b
= b  - b
- b 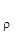 a
a 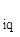 / a
/ a 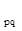 ;a
;a 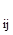 = a
= a 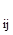 - a
- a 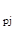 a
a 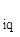 / a
/ a 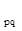 .
.
Задача считается решенной, если в строке целевой функции, не считая свободного члена, нет ни одного положительного элемента (признак оптимальности).
Оптимальное значение каждого фактора z 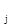 определяют путем потенцирования свободного члена в той же строке. Если в строке целевой функции есть положительный элемент, то соответствующую дополнительную переменную из базиса переводят в свободную, а свободную в базис.
определяют путем потенцирования свободного члена в той же строке. Если в строке целевой функции есть положительный элемент, то соответствующую дополнительную переменную из базиса переводят в свободную, а свободную в базис.
Пример.
Задача: Требуется определить максимум функции
F = x  + x
+ x 
при выполнении следующих ограничений:
x  + 2 x
+ 2 x 
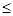 6 ;
6 ;
2 x  + x
+ x 
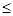 3 ;
3 ;
x  - 2 x
- 2 x 
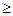 - 1 .
- 1 .
Решение. Приводим ограничения-неравенства к одному виду
x  +2 x
+2 x 
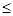 6 ;
6 ;
2 x  + x
+ x 
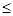 3 ;
3 ;
- x  + 2 x
+ 2 x  £ 1 .
£ 1 .
Заменяем ограничения-неравенства уравнениями, вводя дополнительные переменные y, и полагаем свободный член в целевой функции равным нулю
x  + 2 x
+ 2 x  + y
+ y  = 6 ;
= 6 ;
2 x  + x
+ x  + y
+ y  = 3 ;
= 3 ;
- x  + 2 x
+ 2 x  + y
+ y  = 1 ;
= 1 ;
x  + x
+ x  + y
+ y 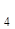 = 0 .
= 0 .
Выражаем значения дополнительных переменных y через основные x
y  = 6 - (x
= 6 - (x  + 2 x
+ 2 x  ) ;
) ;
y  = 3 - (2 x
= 3 - (2 x  + x
+ x  ) ;
) ;
y  = 1 - (- x
= 1 - (- x  + 2 x
+ 2 x  ) ;
) ;
y 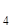 = 0 - (x
= 0 - (x  + x
+ x  ) .
) .
Находим разрешающий элемент в первом столбце коэффициентов и меняем местами основную переменную x  и дополнительную переменную y
и дополнительную переменную y 
2 x  = 3 - ( y
= 3 - ( y + x
 )
)
или
x  = 1,5 - 0,5 y
= 1,5 - 0,5 y  - 0,5 x
- 0,5 x  .
.
Подставляем это значение в остальные уравнения
y  = 6 - (1,5 - 0,5 y
= 6 - (1,5 - 0,5 y  - 0,5 x
- 0,5 x  + 2 x
+ 2 x  ) ;
) ;
x  = 1,5 - (0,5 y
= 1,5 - (0,5 y  + 0,5 x
+ 0,5 x  ) ;
) ;
y  = 1 - (-1,5 + 0,5 y
= 1 - (-1,5 + 0,5 y  + 0,5 x
+ 0,5 x  + 2 x
+ 2 x  ) ;
) ;
y 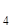 = 0 - (1,5 - 0,5 y
= 0 - (1,5 - 0,5 y  - 0,5 x
- 0,5 x  + x
+ x  ) .
) .
Тогда система уравнений примет вид
y  = 4,5 - (-0,5 y
= 4,5 - (-0,5 y  + 1,5 x
+ 1,5 x  ) ;
) ;
x  = 1,5 - (0,5 y
= 1,5 - (0,5 y  + 0,5 x
+ 0,5 x  ) ;
) ;
y  = 2,5 - (0,5 y
= 2,5 - (0,5 y  + 2,5 x
+ 2,5 x  ) ;
) ;
y 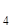 = -1,5 - (-0,5 y
= -1,5 - (-0,5 y  + 0,5 x
+ 0,5 x  ) .
) .
Теперь находим разрешающий элемент во втором столбце и меняем местами основную переменную x  с дополнительной переменной y
с дополнительной переменной y 
2,5 x  = 2,5 - (0,5 y
= 2,5 - (0,5 y  + y
+ y  )
)
или
x  = 1 - 0,2 y
= 1 - 0,2 y  - 0,4 y
- 0,4 y  .
.
Подставляем это значение в остальные уравнения.
y  = 4,5 - (-0,5 y
= 4,5 - (-0,5 y  + 1,5 - 0,3 y
+ 1,5 - 0,3 y  - 0,6 y
- 0,6 y  ) ;
) ;
x  = 1,5 - ( 0,5 y
= 1,5 - ( 0,5 y  + 0,5 - 0,1 y
+ 0,5 - 0,1 y  - 0,2 y
- 0,2 y  ) ;
) ;
x  = 1,0 - (0,2 y
= 1,0 - (0,2 y  + 0,4 y
+ 0,4 y  ) ;
) ;
y 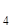 = -1,5 - (-0,5 y
= -1,5 - (-0,5 y  + 0,5 - 0,1 y
+ 0,5 - 0,1 y  - 0,2 y
- 0,2 y  ) .
) .
Тогда система уравнений примет вид
y  = 3 - (-0,8 y
= 3 - (-0,8 y  - 0,6 y
- 0,6 y  ) ;
) ;
x  = 1 - (0,4 y
= 1 - (0,4 y  - 0,2 y
- 0,2 y  ) ;
) ;
x  = 1 - (0,2 y
= 1 - (0,2 y  + 0,4 y
+ 0,4 y  ) ;
) ;
y 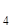 = -2 - (-0,6 y
= -2 - (-0,6 y  - 0,2 y
- 0,2 y  ) .
) .
Так как коэффициенты перед дополнительными переменными y  и y
и y  в строке целевой функции имеют отрицательные значения, то оптимальное решение имеется
в строке целевой функции имеют отрицательные значения, то оптимальное решение имеется
x  = 1 ; x
= 1 ; x  = 1 .
= 1 .
Пример.
Задача: Требуется определить максимум функции F = x  при условии выполнения следующих ограничений:
при условии выполнения следующих ограничений:
x  + 4 x
+ 4 x  £ 16 ;
£ 16 ;
x  - 2 x
- 2 x  ³ - 2 ;
³ - 2 ;
x  + 2 x
+ 2 x  £ 6 ;
£ 6 ;
x  £ 3 .
£ 3 .
Решение. Приводим ограничения-неравенства к одному виду
x  + 4 x
+ 4 x  £ 16 ;
£ 16 ;
- x  + 2 x
+ 2 x  £ 2 ;
£ 2 ;
x  + 2 x
+ 2 x  £ 6 ;
£ 6 ;
x  £ 3 .
£ 3 .
Заменяем ограничения-неравенства уравнениями, вводя дополнительные переменные y и полагая свободный член в целевой функции, равным нулю.
x  + 4 x
+ 4 x  + y
+ y  = 16 ;
= 16 ;
- x  + 2 x
+ 2 x  + y
+ y  = 2 ;
= 2 ;
x  + 2 x
+ 2 x  + y
+ y  = 6 ;
= 6 ;
x  + y
+ y  = 3 ;
= 3 ;
x  + y
+ y 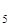 = 0 .
= 0 .
Выражаем значения дополнительных переменных y через основные x
y  = 16 - (x
= 16 - (x  + 4 x
+ 4 x  ) ;
) ;
y  = 2 - (-x
= 2 - (-x  + 2 x
+ 2 x  ) ;
) ;
y  = 6 - (x
= 6 - (x  + 2 x
+ 2 x  ) ;
) ;
y  = 3 - (x
= 3 - (x  ) ;
) ;
y 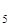 = 0 – ( x
= 0 – ( x  ) .
) .
Находим разрешающий элемент в первом столбце коэффициентов и меняем местами основную переменную x  с дополнительной переменной y
с дополнительной переменной y 
x  = 3 - y
= 3 - y  .
.
Подставляем это значение в остальные уравнения
y  = 16 - ( 3 - y
= 16 - ( 3 - y  + 4 x
+ 4 x  ) ;
) ;
y  = 2 - (-3 + y
= 2 - (-3 + y  + 2 x
+ 2 x  ) ;
) ;
y  = 6 - ( 3 - y
= 6 - ( 3 - y  + 2 x
+ 2 x  ) ;
) ;
x  = 3 - ( y
= 3 - ( y  ) ;
) ;
y 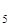 = 0 - ( x
= 0 - ( x  ) .
) .
Тогда система уравнений примет вид
y  = 13 - (-y
= 13 - (-y  + 4 x
+ 4 x  ) ;
) ;
y  = 5 - ( y
= 5 - ( y  + 2 x
+ 2 x  ) ;
) ;
y  = 3 - (-y
= 3 - (-y  + 2 x
+ 2 x  ) ;
) ;
x  = 3 - ( y
= 3 - ( y  ) ;
) ;
y 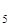 = 0 - ( x
= 0 - ( x  ) .
) .
Теперь находим разрешающий элемент во втором столбце и меняем местами основную переменную x и дополнительную y
2 x  = 3 - (- y
= 3 - (- y  + y
+ y  )
)
или
x  = 1,5 + 0,5 y
= 1,5 + 0,5 y  - 0,5 y
- 0,5 y  .
.
Подставляем это значение в остальные уравнения
y  = 13 - ( - y
= 13 - ( - y  + 6 + 2 y
+ 6 + 2 y  - 2 y
- 2 y  ) ;
) ;
y  = 5 - ( y
= 5 - ( y  + 3 + y
+ 3 + y  - y
- y  ) ;
) ;
x  = 1,5 - (-0,5y
= 1,5 - (-0,5y  + 0,5y
+ 0,5y  ) ;
) ;
x  = 3 - ( y
= 3 - ( y  ) ;
) ;
y 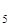 = 0 - ( 1,5 + 0,5y
= 0 - ( 1,5 + 0,5y  - 0,5y
- 0,5y  ) .
) .
Тогда система уравнений примет вид
y  = 7 - ( y
= 7 - ( y  - 2 y
- 2 y  ) ;
) ;
y  = 2 - ( 2 y
= 2 - ( 2 y  - y
- y  ) ;
) ;
x  = 1,5 - (-0,5 y
= 1,5 - (-0,5 y  + 0,5 y
+ 0,5 y  ) ;
) ;
x  = 3 - ( y
= 3 - ( y  ) ;
) ;
y 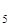 = -1,5 - ( 0,5 y
= -1,5 - ( 0,5 y  - 0,5 y
- 0,5 y  ) .
) .
Так как в строке целевой функции коэффициент перед дополнительной переменной y  положительный, то решение x
положительный, то решение x  = 3 и x
= 3 и x  = 1,5 не оптимально.
= 1,5 не оптимально.
Поэтому в столбце коэффициентов перед y  находим разрешающий элемент и относительно его меняем местами дополнительные переменные y
находим разрешающий элемент и относительно его меняем местами дополнительные переменные y  и y
и y 
2 y  = 2 - ( y
= 2 - ( y  - y
- y  )
)
или
y  = 1 - 0,5 y
= 1 - 0,5 y  + 0,5 y
+ 0,5 y  .
.
Подставляем это значение в остальные уравнения
y  = 7 - ( 1 - 0,5 y
= 7 - ( 1 - 0,5 y  + 0,5 y
+ 0,5 y  - 2 y
- 2 y  ) ;
) ;
y  = 1 - ( 0,5 y
= 1 - ( 0,5 y  - 0,5 y
- 0,5 y  ) ;
) ;
x  = 1,5 - (-0,5 + 0,25 y
= 1,5 - (-0,5 + 0,25 y  - 0,25 y
- 0,25 y  + 0,5 y
+ 0,5 y  ) ;
) ;
x  = 3 - ( 1 - 0,5 y
= 3 - ( 1 - 0,5 y  + 0,5 y
+ 0,5 y  ) ;
) ;
y 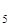 = -1,5 - (0,5 - 0,25 y
= -1,5 - (0,5 - 0,25 y  + 0,25 y
+ 0,25 y  - 0,5 y
- 0,5 y  ) .
) .
Тогда система уравнений примет вид
y  = 6 - (-0,5 y2 - 1,5 y3) ;
= 6 - (-0,5 y2 - 1,5 y3) ;
y  = 1 - (0,5 y2 - 0,5 y3) ;
= 1 - (0,5 y2 - 0,5 y3) ;
x  = 2 - (0,25 y2 + 0,25 y3) ;
= 2 - (0,25 y2 + 0,25 y3) ;
x  = 2 - (-0,5 y2 + 0,5 y3) ;
= 2 - (-0,5 y2 + 0,5 y3) ;
y 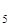 = -2 - (-0,25 y2 - 0,25 y3) .
= -2 - (-0,25 y2 - 0,25 y3) .
Так как коэффициенты перед дополнительными переменными y  и y
и y  в строке целевой функции отрицательные, то оптимальное решение найдено. Это x
в строке целевой функции отрицательные, то оптимальное решение найдено. Это x  = 2 ; x
= 2 ; x  = 2.
= 2.
8.7. Стохастическое программирование
Сравнение задачи стохастического программирования с задачей линейного программирования для детерминированных величин показывает, что детерминированный эквивалент задачи стохастического программирования отличается от задачи линейного программирования уменьшением допустимых значений параметров процесса ln [R 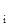 ] на некоторую величину (1/
] на некоторую величину (1/ 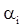 ) ln ln (1/(1- F(R
) ln ln (1/(1- F(R 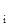 ))). Эта величина определяется требуемой вероятностью работоспособного состояния F(R
))). Эта величина определяется требуемой вероятностью работоспособного состояния F(R 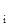 ) и показателем распределения случайного параметра
) и показателем распределения случайного параметра 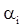 . Она является платой за принятие решения об управлении в условиях неопределенности.
. Она является платой за принятие решения об управлении в условиях неопределенности.
Возможно, эта плата окажется неиспользованной, но для достижения цели она необходима.
Детерминированный эквивалент задачи стохастического программирования решается симплекс-методом. Если число неизвестных управляющих факторов равно двум, то эта задача может быть решена графически. Для этого в логарифмических координатах строят семейство прямых, уравнения которых имеют вид
ln z 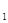 = b
= b 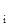 / a
/ a 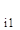 - (a
- (a 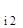 / a
/ a 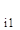 ) ln z
) ln z  ,
,
где b 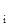 = ln R
= ln R 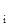 - ln c
- ln c 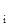 - (1 /
- (1 / 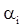 ) lnln (1 / (1-F (R))) .
) lnln (1 / (1-F (R))) .
Каждая их этих прямых является границей "допустимой полуплоскости", все точки которой (z1 и z2) удовлетворяют ограничениям-неравенствам. Часть плоскости, принадлежащая одновременно всем "допустимым полуплоскостям", образует область "допустимых решений". Все точки этой области удовлетворяют всем без исключения ограничениям-неравенствам.
Далее строят "основную прямую", уравнение которой
ln z 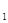 = - (a
= - (a 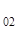 / a
/ a 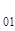 ) ln z
) ln z 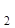 ,
,
и определяют направление ее возрастания. “Основную прямую” перемещают в этом направлении параллельно самой себе до тех пор, пока она не будет иметь с "областью допустимых решений" только одну общую точку. Потенцируя координаты этой точки, получают оптимальные значения z  и z
и z  .
.
|

