Характерной особенностью некоторых социально-экономических процессов, представленных временными рядами, является ярко выраженная периодичность. Например, интенсивность транспортных поездок (особенно на длинные расстояния) резко возрастает в летние месяцы и снижается в межсезонные периоды. Интенсивность посещений зрелищных мероприятий значительно выше в зимний период, когда большинство населения находится дома, и падает в летнее время, когда люди, как правило, находятся в отпусках.
Сезонная периодичность характерна и для курсов валют. В РФ спрос на валюту (и соответственно ее цена) обычно растет к концу года, когда подходят сроки платежей, и снижается в летний период, когда деловая активность падает.
Сезонные колебания часто сочетаются с более общей тенденцией процесса, характеризующейся, например, ростом среднегодовых (среднеквартальных и т. п.) его значений. В такой ситуации иногда рекомендуется общую модель процесса представить в виде трех составляющих: “тренда”, выражающего общую тенденцию; “сезонной компоненты”, описывающей сезонные колебания вокруг этого тренда, и “случайной компоненты”, традиционно выражающей свойства ошибки. Однако такой подход к формированию общей модели, как правило, не является экономичным, в том смысле, что эта модель может содержать слишком много параметров, которые оцениваются с большой ошибкой. Особенно это относится к параметрам трендовых моделей, ошибки оценок которых обусловлены значительными отклонениями реальных данных от трендов именно из-за наличия сезонных эффектов. Вследствие этого такая модель может не обладать достаточной точностью. Кроме того, наличие тренда во временном ряду может быть вызвано какими-либо систематическими эффектами. Например, ежегодный рост туристических поездок – увеличением доходов населения. В данном случае в модели может появиться систематическая ошибка, обусловленная недостаточной точностью аппроксимации временным трендом тенденции роста дохода.
Большое число параметров характерно и для моделей, описывающих “собственно” сезонные колебания. Обычно такая модель представляется в виде набора синусоид и косинусоид
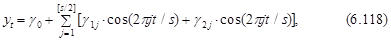
где g0, g1j и g2j – коэффициенты модели; s – общий период колебания,
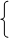 1/2 s – для четных s;
1/2 s – для четных s;
[s/2]= 1/2 (s–1) – длячетныхs;
индексы j и t определяют фазу колебательного процесса.
При построении моделей временных рядов типа АРСС(k, m) – авторегрессии–скользящего среднего – одним из критериев их качества (пусть и неформальным) является минимум параметров. Как было отмечено выше, меньшее число параметров модели способствует повышению ее устойчивости, часто ведет к уменьшению ошибки прогноза. В этой связи достаточно плодотворной оказалась идея уменьшения числа параметров модели временных рядов, описывающих процессы с сезонными колебаниями, путем учета при их построении взаимосвязей не только между соседними значениями процесса, но и между его значениями, разделенными периодом колебания. Кроме того, реализация этой идеи показала возможность рассмотрения моделей временных рядов с сезонными колебаниями как специфической подгруппы моделей АРСС(k, m). Модели данной подгруппы называют также мультипликативными моделями временных рядов.
Рассмотрим общую идею их построения на содержательном уровне чуть более подробно. Если временной ряд характеризуется сезонной составляющей с периодом s, то в таком ряду обычно выделяют два различных типа взаимосвязей между переменными – текущую и сезонную. Текущая взаимосвязь, как и ранее, характерна для соседних значений временного ряда уt и уt–1, уt–2,..., сезонная – для значений, разделенных периодом колебаний уt и уt–s. Так, например, если временной ряд выражает ежемесячные значения какого-либо процесса, а сезонная его составляющая имеет период колебания 12, то s=12. В таком случае разность уt–уt–s, может быть определена следующим выражением:
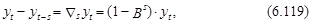
где Вs – оператор сдвига на s периодов, т. е. Вs уt =уt–s.
Предположим, что разность (6.119) является стационарным процессом, который может быть описан моделью, относящейся к классу моделей АРСС(k, m), например, моделью АР(1):
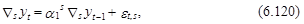
где et,s – ошибка такой модели, a1s – ее коэффициент.
Переписывая модель (6. 120) с учетом операторов сдвига В и Вs, получим ее выражение в виде произведения двух операторов (мультипликативная связь)
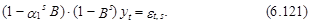
В развернутом виде выражение (6.121) связывает текущее значение процесса уt с его предшествующим значением уt–1 и значениями прошлого периода уt–s и уt–s–1:
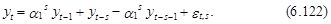
Идентификация мультипликативной модели в данном случае осуществляется на основании анализа автокорреляционной функции процесса (1–Вs)уt. В случае модели (6.122) коэффициенты автокорреляции разностей уt–уt–s должны обладать свойствами автокорреляционной функции модели АР(1).
Аналогично, если разность (6.119) может быть представлена в виде модели скользящего среднего первого порядка, связывающего прирост Ñsуt с приростом белого шума при том же периоде колебаний
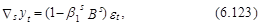
где b1S – коэффициент модели, а соседние разности Ñуt и Ñуt–1 связаны той же моделью, но с коэффициентом b1, то мультипликативная модель записывается в следующем виде:
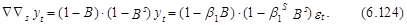
В развернутой форме выражение (6.124) имеет следующий вид:
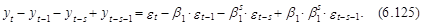
Идентификация модели типа (6.124) базируется на свойствах функции автокорреляции процесса (1–В)(1–Вs)уt . Заметим, что у него ненулевыми являются коэффициенты автокорреляции, соответствующие только задержкам 1, 11, 12 и 13. Значения данных коэффициентов несложно определить на основе соответствующих ковариаций* :
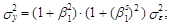
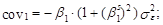

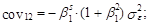
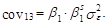
Таким образом, идентификация моделей временных рядов с сезонными колебаниями в общем случае предполагает анализ корреляционных взаимосвязей двух типов: между соседними значениями процесса и между значениями, разделенными предполагаемым периодом колебаний. При этом речь может идти и о процессе, подвергнутом предварительному преобразованию (см. выражения (6.39)–(6.42)).
Отметим также, что в общем случае при наличии сезонных колебаний процесс уt, как правило, характеризуется высокими значениями коэффициентов автокорреляции даже при больших задержках. Преобразование процесса с целью исключения тренда (например, путем перехода к конечным разностям) обычно ведет к тому, что упреобразованного процесса значительно выделяются по величине автокорреляции кратные периоду колебания. Это, как раз, и указывает на присутствие сезонной составляющей.
Процедуры оценки коэффициентов моделей временных рядов с сезонными колебаниями базируются на тех же причинах, что и процедуры оценки моделей временных рядов общего типа. В их основе лежит критерий минимизации суммы квадратов ошибки. Однако получить аналитические выражения для оценок их коэффициентов (типа решений Юла-Уокера и т. п.) в общем случае достаточно сложно. Вследствие этого на практике обычно используют методы нелинейного оценивания параметров таких моделей, базирующиеся на итеративных процедурах последовательного приближения оценок к их оптимальному значению (см. главу XI). Заметим при этом, что приблизительные (начальные) оценки параметров моделей могут быть оценены отдельно для процесса образованного соседними значениями и для процесса. образованного его значениями, разделенными периодом колебаний в соответствии с известными процедурами оценки моделей типа АРСС(k, m).
В целом, построение модели временного ряда с сезонными колебаниями осуществляется по традиционной схеме, которая состоит из следующих этапов:
1. На основании анализа исходного процесса (исследования свойств стационарности, вида автокорреляционной функции) выводится суждение о наличие трендовой составляющей.
2. В случае необходимости с помощью подходящего преобразования тренд исключается из рассматриваемого временного ряда.
3. Для оставшейся стационарной составляющей по виду ее автокорреляционной функции подбирается “подходящий” вариант модели.
4. На основании значений соответствующих выборочных коэффициентов автокорреляции определяют предварительные начальные оценки параметров моделей. Применяя более сложные процедуры оценивания, эти оценки затем уточняют.
5. Определяется ряд ошибок модели, на основании анализа свойств которого, выбранный вариант модели либо уточняется (улучшается), либо принимается в качестве окончательного решения.
