Обеспечение адекватности модели при моделировании является одной из главных проблем. В данном случае следует иметь в виду, что наилучшей моделью является сама система. Если создается модель, то она не обязательно должна отображать все свойства системы. Очевидно, чем синтезированная модель более адекватна самой системе, тем она более сложна и тем сложнее с ней работать. Из другой стороны: избыточная упрощенность модели приводит к потере адекватности. Здесь главную роль играет интуиция и опыт исследователя, которые дают возможность находить то главное, что должна отображать синтезируемая модель.
Вместе с тем, существуют и некоторые объективные характеристики, которые следует учитывать при выборе сложности модели. Известно, что не всякая семантическая информация, поступающая к человеку, может вызывать соответствующую реакцию, а только осознанная и такая, “что оставила след” в ее памяти. В основе такого расчета лежат две гипотезы, основанные на изучении особенностей восприятия человеком информации.
Гипотеза 1. Количество информации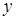 
, зафиксированное памятью человека, связано с количеством входящей информации 
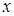логарифмической функцией:
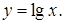(3.4)
Из (3.4) следует, что с увеличением объема информационного потока рост количества информации, зафиксировавшейся в памяти человека, замедляется, то есть избыточное количество поступающей информации не имеет смысла.
Гипотеза 2. Представление о предмете познания связано с количеством входной информации о нем нелинейной асимптотической функцией
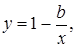(3.5)
где 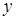– представление о предмете познания; 
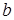– порог чувствительности относительно поступающей информации (можно взять 
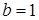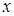); – количество входящей информации о предмете.
Из (3.5) следует, что наши познания о предмете монотонно растут с ростом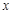 
, приближаясь к 1 (к полному представлению) асимптотически. Если сначала модификация функции (3.5) слишком заметна, то по мере роста x она резко замедляется.
Особенными точками функций в (3.4) и (3.5) являются точки (1,0), где они равны нулю. Это означает, что один неизолированный факт не несет информации и представление о предмете не формирует. Два факта, в соответствии с (3.4), дадут уровень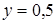 
. Дальше идет более замедленный, хоть и монотонный рост обеих функций. Точка является корнем двух уравнений (3.4) и (3.5), что, возможно, свидетельствует о достаточной полноте входной информации. Возможно, что с этим связан жизненный опыт, в соответствии с которым максимальное количество собеседников за столом, или на пикнике, когда еще поддерживается единство интересов, составляет 8 человек.
Две рассмотренные гипотезы могут быть использованы при синтезе моделей систем для оценки полноты и достаточности информации о системе, закладываемой в синтезируемую модель.
Таким образом, процесс создания модели и самого исследования модели является творческим процессом, в каждом конкретном случае имеет свою специфику, конкретные трудности и пути достижения конечной цели. Попытка как-то направить или ограничить этот процесс носит больше вид рекомендаций или советов, чем алгоритма действий. Все же приведем схему исследования модели, которое также носит достаточно общий характер. Такая схема показана на рис. 3.1. Она отображает логику действий, начиная от исходной проблемной ситуации к использованию синтезированной модели.
3.2.9. Модельное исследование, как и какой-либо иной тип осознанной целенаправленной деятельности, начинается с попытки изменить в лучшую сторону ситуацию в какой-то отрасли. Поэтому в схеме на рис. 3.1 исходная проблемная ситуация непосредственно связана с конечной целью или системой таких целей. Для индикации того, насколько создаваемая экспериментальная модель адекватна реальной системе и насколько она имеет практическую пригодность, формулируется критерий согласия, связанный как с выбором объекта моделирования, так и с самой синтезированной моделью.
В распоряжении исследователя могут быть аналитические, экспериментальные или имитационные средства моделирования, в результате использования которых и синтезируется модель. Часто экспериментальную модель синтезируют на основе гистограммы распределений. Особенную сложность при этом вызывает формализированное описание модели и принятие решения о ее качестве.
Для сравнения экспериментальной модели с теоретической (часто с нормальным законом) используют критерии информационной меры, меры Кульбака.
Критерий согласия (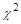 
-критерий)
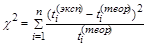
где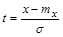 
- нормированное значение СВ
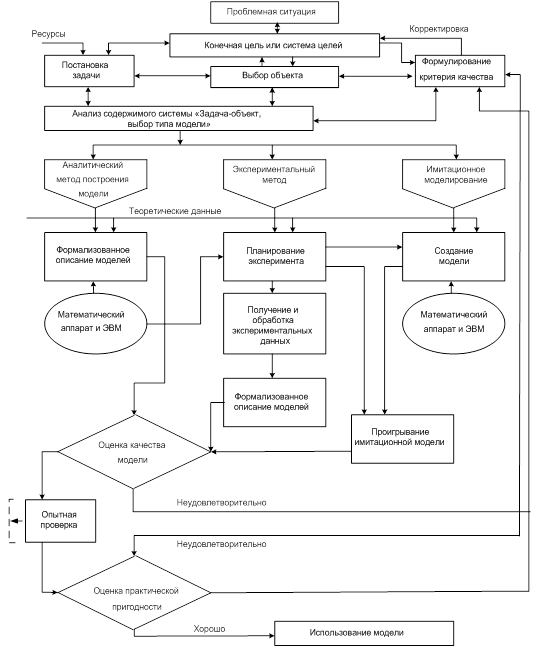
Рис. 3.1. Схема проведения модельного исследования
Теорема Бернули гласит: при неограниченном числе испытаний математическая оценка 
сходится по вероятности к истинному значению:
.
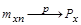Другим названием теоремы является закон больших чисел.