Предельное распределение и численные значения предельного распределения компонент определяется стохастической матрицей W.
Система для которой предельный вектор существует, называют эргодической. Рассмотрим стохастическую матрицу W. Если некоторый элемент wij этой матрицы отличен от нуля, переход из состояния i в состояние j возможен за один шаг. Множество всех состояний системы и выполнимых переходов очень удобно отображать в виде графа.
Граф есть совокупность вершин, соединенных непрерывными дугами. Соответствие между множеством состояний и возможных переходов системы, с одной стороны, и множеством вершин и дуг графа, с другой, установим следующим образом. Множество состояний системы отображается совокупностью вершин графа, а возможные переходы системы – в виде дуг графа, причем направление дуги указывает, из какого состояния и в какое переходит система. Каждой дуге графа припишем число, равное соответствующей вероятности перехода системы за один шаг. Матрице переходов системы W и ее граф взаимно однозначно соответствуют друг другу.
Управляемые марковские цепи
Как указывалось выше, под управляемыми марковскими процессами понимают такие, у которых имеется возможность до определенной степени управлять значениями переходных вероятностей. В качестве примеров таких процессов можно привести любые торговые операции, у которых вероятность сбыта и получения эффекта может зависеть от рекламы, мероприятий по улучшению качества, выбора покупателя или рынка сбыта и т.д.
В лесной отрасли эффективность может зависеть, например, от региональной лесомелиорации, оптимальной стратегии лесопользования (рубки ухода, технологические приемы, комплекс машин, дорожная сеть и т.д.)
Очевидно, что при создании математических моделей в данном случае должны фигурировать следующие компоненты:
· конечное множество решений (альтернатив) Ki ,
где i Î S - номер состояния системы;
· матрицы переходов П[s](k), соответствующие тому или иному принятому к-решению;
- матрицы доходов (расходов) R[s](k), также отражающие эффективность данного решения.
Управляемой цепью Маркова(УЦМ) называется случайный процесс, обладающий марковским свойством и включающий в качестве элементов математической модели конструкцию (кортеж) < Ki , П[s](k) , R[s](k) > . Решение, принимаемое в каждый конкретный момент (шаг процесса) назовем частным управлением.
Таким образом, процесс функционирования системы описываемой УЦМ, выглядит следующим образом:
· если система находится в состоянии i Î S и принимается решение k Î K i то она получает доход ri(k);
- состояние системы в последующий момент времени (шаг) определяется вероятностью P ij(k), то есть вероятность того, что система из состояния i
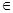 S перейдет в состояние j
S перейдет в состояние j S , если выбрано решение K i.
Очевидно, общий доход за n-шагов является случайной величиной, зависящей от начального состояния и качества принимаемых в течение хода процесса решений, причем это качество оценивается величиной среднего суммарного дохода (при конечном времени) или среднего дохода за единицу времени (при бесконечном времени).
Стратегией p называется последовательность решений:
p = ( f 1, f 2, .... f n) , (4)
где
f n = < k1, k2, .... kn> Î k - вектор управления.
Задание стратегии означает полное описание конкретных решений, принимаемых на всех шагах процесса в зависимости от состояния, в котором находится в этот момент процесс.
Если в последовательности (вектора) p все f одинаковы, то такая стратегия называется стационарной, т.е. не зависящей от номера шага. Стратегия p = ( f 1, f 2, .... f n) называется марковской, если решение f n принимаемое в каждом конкретном состоянии зависит только от момента времени n, но не зависит от предшествующих состояний.
Оптимальной будет такая стратегия, которая максимизирует полный ожидаемый доход для всех i и n. В теории УМЦ разработаны два метода определения оптимальных стратегий: рекуррентный и итерационный.
Первый, рекуррентный метод, применяется чаще всего при сравнительно небольшом числе шагов n. Его идея основана на применении принципа Беллмана и заключается в последовательной оптимизации дохода на каждом шаге с использованием рекуррентного уравнения.
Таким образом, данный метод, по существу, аналогичен методу динамического программирования, отличием является лишь то, что на каждом шаге учитывается вероятность попадания системы в то или иное состояние. Поэтому этот метод называют стохастическим динамическим программированием.
Конкретное применение метода будет рассмотрено ниже на примере.
Второй - итерационный метод оптимизации применяется при неограниченном числе этапов (шагов) процесса. Этот метод использует свойство эргодичности марковской цепи и заключается в последовательном уточнении решения путем повторных расчетов (итераций). При этих уточнениях находят решение, обеспечивающее в среднем минимум дохода при большом числе шагов. Оно уже не будет зависеть от того, на каком шаге производится оценка оптимальной стратегии, то есть является справедливым для всего процесса, независимо от номера шага. Важным достоинством метода является, кроме того, и то, что он дает возможность определить момент прекращения дальнейших уточнений.
Главным отличием итерационного метода от рассмотренного выше, рекуррентного, заключается в том, что в данном случае используется матрица предельных (финальных) вероятностей, где вследствие свойства эргодичности переходные вероятности постоянны на всех шагах процесса. Поскольку матрица доходов состоит также из постоянных, не зависимых от n величин, то можно предположить, что с ростом n общая величина доходов будет возрастать линейно.
Лекция №4
