В таблице 6.1 представлены все булевы функции двух переменных.
Таблица 6.1
| x1 | x2 | f0 | f1 | f 2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
В таблице 6.2 представлены названия и даны пояснения по каждой из 16 функций.
Таблица 6.2
| Ф-ция | Название | Описание через ˄,˅,ˉ | Читается, как… |
| f0 | константа Æ | Æ | Æ |
| f1 | конъюнкция x1 и x2 |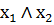 
| х1 и х2 |
| f2 | отрицание по х2 |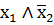 
| неверно, что если х1, то х2 |
| f3 | переменная х1 | 
| х1 |
| f4 | отрицание по х1 |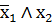 
| неверно, что если х2, то х1 |
| f5 | переменная х2 |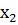 
| х2 |
| f6 | сумма по mod 2 (х1Åх2) |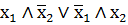 
| х1 неравнозначно х2 |
| f7 | дизъюнкция x1 и x2 |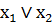 
| х1 или х2 |
| f8 | стрелка Пирса х1 ¯ х2 |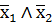 
| ни х1, ни х2 |
| f9 | эквиваленция х1~х2 |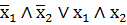 
| х1 равнозначно х2 |
| f10 | отрицание х2 |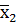 
| не х2 |
| f11 | импликация по х2 (х2®x1) |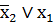 
| если x2, то x1 |
| f12 | отрицание х1 |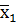 
| не х1 |
| f13 | импликация по х1 (x1 ® х2) |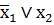 
| если x1, то x2 |
| f14 | штрих Шеффера (x1|x2) |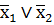 
| не верно, что х1 и х2 |
| f15 | константа 1 |
Пример:
Используя табличный редактор MS Excel определить значения функции, соответствующие следующим формулам:
x1 ® х2 и х1~х2
Для этого в ячейки MS Excel C2 и D2, соответствующие набору х1=0 и х2=0, вводятся формулы:
=(B2>=A2)*1 (для x1 ® х2)
=(A2=B2)*1 (для х1~х2)
Затем эти формулы распространяются на весь оставшийся диапазон C3:D5. В итоге формируется итоговая таблица (рисунок 6.1).
Рисунок 6. 1 Экранная форма MS Excel с итоговой таблицей
Построение СДНФ и СКНФ функции
Кроме табличного задания функции алгебры логики применяются различные аналитические методы. К ним относятся – дизъюктивная и коньюктивная форма.
Набор значений переменных можно обобщенно представить, как последовательность констант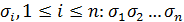 
.
Введем условное обозначение:
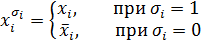
| (6.1) |
где совокупность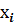 
– порождающие множества;
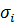– первичный терм;
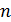– число порождающих множеств.
Произведение вида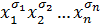 
называют элементарной конъюнкциейи записывают в векторной форме следующим образом:
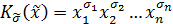
| (6.2) |
В такой записи вектор переменных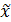 
определяет, какие переменные образуют конъюнкцию, а набор 
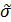задает порядок расстановки знаков инверсии (отрицания) над ними.
Формула вида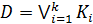 
, где 
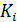- различные элементарные конъюнкции, называется дизъюнктивной нормальной формой (ДНФ).
При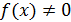 
тождественно, ее можно представить в виде:
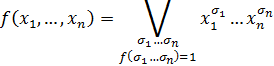
| (6.3) |
Такое разложение функции носит название совершенной дизъюнктивной нормальной формы (СДНФ). Т.е. совершенной ДНФ (СДНФ) называется ДНФ, в которой нет равных элементарных конъюнкций, и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием).
Длина СДНФ равна числу наборов, на которых функция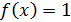 
.
Алгоритм построения СДНФ:
1) Выбрать в таблице функции все наборы аргументов, на которых функция обращается в единицу
2) Вычислить конъюнкцию, соответствующей этим наборам аргументам. При этом аргумент xi входит в данный набор как 1 , он вписывается без изменения в конъюнкцию, соответствующую данному набору. Если хi входит как 0, то в конъюнкцию вписывается его отрицание.
3) Все полученные конъюнкции соединены между собой знаками дизъюнкции.
Соответственно выражение
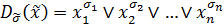
| (6.4) |
где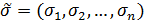 
– какой-либо двоичный набор, причем среди переменных 
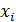могут быть совпадающие, называется элементарной дизъюнкцией.
Формула вида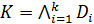 
, где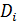 
- различные элементарные дизъюнкции, называется конъюнктивной нормальной формой (КНФ). Т.е. всякую конъюнкцию элементарных дизъюнкций называют конъюнктивной нормальной формой, то есть КНФ.
При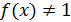 
тождественно, ее можно представить в виде:
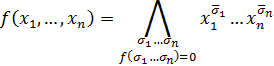
| (6.5) |
Такое разложение функции носит название совершенной конъюнктивной нормальной формы (СКНФ). Т.е. совершенной КНФ (СКНФ) называется КНФ, в которой нет равных элементарных дизъюнкций, и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием).
Так как существует взаимно однозначное соответствие между таблицей истинности и СДНФ (СКНФ) функции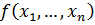 
, то СДНФ (СКНФ) – единственна.
Пример: Построить СДНФ и СКНФ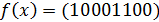 
| x1 | x2 | x3 |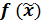 
|
СДНФ:
,
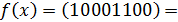
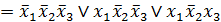СКНФ:
.
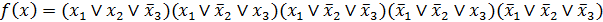