В настоящее время рассматривают три механизма роста металлических кристаллов:
-флуктуационный
-дислокационный
-нормальный
Флуктуационный механизм роста.
 Перемещение плоской грани происходит в результате многократного образования зародышей роста с высотой δ, в результате чего поверхность зарастает полностью и перемещается на величину δ. Критическим моментом является появление первого зародыша роста, работа образования которого существенно больше, чем зародышей, которые к нему подстраиваются.
Перемещение плоской грани происходит в результате многократного образования зародышей роста с высотой δ, в результате чего поверхность зарастает полностью и перемещается на величину δ. Критическим моментом является появление первого зародыша роста, работа образования которого существенно больше, чем зародышей, которые к нему подстраиваются.
∆G=-∆Gv+∆Gs=-∆ϕ  πr2δ+Ϭ
πr2δ+Ϭ  2πrδ;
2πrδ;
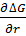 =-∆ϕ
=-∆ϕ  2 πrδ+Ϭ
2 πrδ+Ϭ  2πδ=0
2πδ=0
(Vкр)р= Ϭ/∆ϕ= 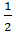 rскрв
rскрв
Кристаллический зародыш роста имеет радиус в два раза меньше зародышей вынужденных и самопроизвольных.
(∆Gркр)= -∆ϕ  π
π 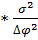
 Ϭ+Ϭ
Ϭ+Ϭ  2π
2π 
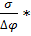 Ϭ=
Ϭ= 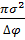 (-1+2);
(-1+2);
(∆Gркр)= 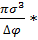 δ; δ=
δ; δ= 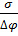 ; (∆Gркр)=
; (∆Gркр)= 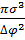 ;
;
V=N0  exp(
exp( 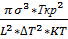 ); N0’-количество атамов, распологающихся на поверхности одного поля кристаллизующегося вещества.
); N0’-количество атамов, распологающихся на поверхности одного поля кристаллизующегося вещества.
∆ T’’’ 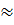 0
0
∆T<∆T ‘’’– если зародышей нет - они не образуются, если зародыши есть- зародыши не будут расти
∆T’’>∆T>∆T’’’- если зародыши есть- они будут расти.
∆T’>∆T>∆T’’-появляются вынужденные зародыши и возможен рост новых зародышей.
∆T<∆T’-появляются вынужденные и самопроизвольные зародыши, происходит рост всех зародышей.
Флуктуационный механизм роста характерен для веществ с гладкими гранями, то есть обладающих высоким значением изменения энтропии при кристаллизации. Это вещества, которые являются химическими соединениями или обладающие ковалентной связью. Такими в литейных сплавах являются: графит в чугунах, кремний в силуминах и интерметаллиды.
Дислокационный механизм роста.
Характерен для условий, когда образующаяся твердая фаза за счет деформаций имеет большую плотность дислокаций, в частности винтовых, которые играют важную роль в перемещении кристаллических граней при сохранении самих дислокаций.
V=K*∆T2 В условиях кристаллизации промышленных сплавов дислокационный рост является редким явлением.
Нормальный механизм роста.
Характерен для веществ с малой энтропией, то есть для веществ с малыми межатомными связями. В результате чего поверхность раздела между металлом и расплавом носит диффузионный характер.

Присоединение зародыша роста происходит с равной вероятностью в любой точке поверхности раздела. Такой механизм роста характерен для условий малого переохлаждения расплава, составляющего единицы градусов V=k∆T.
Таким образом, процесс роста не имеет порогового переохлаждения, и реальный рост металлических кристаллов происходит при сколь угодно малых переохлаждениях. Величина К для металлов чрезвычайно велика.
Термодинамический анализ процесса кристаллизации свидетельствует, что преимущественным процессом образования центров кристаллизации в металлургических расплавах является вынужденное зарождение на включениях, активность которых определяется родством структуры с основным металлом. Самопроизвольная кристаллизация играет второстепенную роль, так как требует значительно больших переохлаждений и выступает на передний план когда вынужденная кристаллизация подавлена или протекает в малой степени.Как образование зародышей, так и их рост являются интенсивными функциями переохлаждения расплава.
L  ∆m=с
∆m=с  ∆T; ∆m=с*
∆T; ∆m=с* 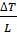 ;
;  = 0.002
= 0.002  ;
;
∆m=0,002  ∆T
∆T
∆T=10К; ∆m=2%.
Кристаллизация возможно только в условиях непрерывного отвода выделяющейся теплоты и, значит, кинетика кристаллизации диктуется теплоотводом.
Кинетика кристаллизации
Кинетика изотермической кристаллизации

N3=const; ʋ=const; ∆T=const;
dv= ʋ  dί; v= ʋ
dί; v= ʋ  ί;
ί;
V1= 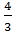 π
π  r3=
r3= 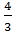 π
π  ʋ3
ʋ3  ί3;
ί3;
Vт=V1*N3= 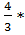 N3*ʋ3
N3*ʋ3  ί3; ίкр=
ί3; ίкр= 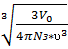 ;
;
V0=  π
π  N3
N3  ʋ3
ʋ3  ί3кр;
ί3кр;
Кинетика кристаллизации ансамбля растущих зародышей осложняется их смыканием. С некоторого момента, когда площадь по которой происходит прирост твердой фазы, то есть их площадьграничещая с жидкой фазой начинает непрерывно сокращаться, и к моменту окончания кристаллизации превращается в нуль. Кристаллизация происходит в два этапа:
1)Объем возрастает пропорционально кубу времени в условиях свободного роста.
2) Этап ограниченного роста, скорость прироста твердой фазы непрерывно сокращается.
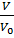 =1-exp(-K ίn); n”=3.05; n’=3.98
=1-exp(-K ίn); n”=3.05; n’=3.98
Первая задача Колмогорова
Изотермическая кристаллизация на вынужденных зародышах
∆T=const; Nc=0; N=Nз; ʋ =const;
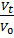 =1-exp(
=1-exp( 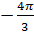 *N3ʋ3ί3);
*N3ʋ3ί3);
e-x=1-x; 1-1+ 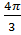 N3ʋ3ί3. (N ʋ3)”’>(N ʋ3)”>(N ʋ3)’
N3ʋ3ί3. (N ʋ3)”’>(N ʋ3)”>(N ʋ3)’

Аргументом этого уравнения является произведение числа зародышей на скорость их роста в кубе. Чем больше это произведение, тем быстрее завершается кристаллизация.
Расчитаем скорость прироста твердой фазы:
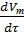 =[-exp]
=[-exp]  (-
(- 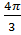 )
)  N3
N3  ʋ3
ʋ3  3ί2=(1-
3ί2=(1- 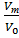 )
)  4π
4π  N3
N3  ʋ2
ʋ2  ί2
ί2  ʋ= [4 πr2
ʋ= [4 πr2  N3]
N3] 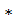 ʋ(1-
ʋ(1- 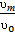 )=S’
)=S’  V(1-
V(1- 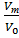 );
);
S’- поверхность свободно растущих сферических кристаллов, несмыкающихся друг с другом. Она увеличевается во времени пропорционально ί2
(1- 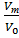 )- оставшаяся доля жидкой фазы. Этот член непрерывно уменьшается и превращается в нуль.
)- оставшаяся доля жидкой фазы. Этот член непрерывно уменьшается и превращается в нуль.
 Скорость прироста твердой фазы на начальном этапе непрерывно возрастает в результате увеличения поверхности роста кристаллизации S’.
Скорость прироста твердой фазы на начальном этапе непрерывно возрастает в результате увеличения поверхности роста кристаллизации S’. 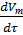
После смыкания кристаллов непрерывно уменьшается до 0 в результате сокращения объема жидкой фазы.
Вторая задача Колмогорова:
Изотермическая кристаллизация на самопроизвольных зародышах:
∆T=const; Nc=0; N=Nз; ʋ =const
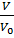 =1-exp(-
=1-exp(- 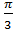 nʋ3
nʋ3 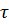 4) (nʋ3)’’’>(nʋ3)’’>(nʋ3)’.
4) (nʋ3)’’’>(nʋ3)’’>(nʋ3)’.
 Чем больше параметр самопроизвольной кристаллизации (nʋ3), тем быстрее завершается кристаллизация и выше скорость выделения твердой фазы в момент ее максимума.
Чем больше параметр самопроизвольной кристаллизации (nʋ3), тем быстрее завершается кристаллизация и выше скорость выделения твердой фазы в момент ее максимума.
ίкр=?; 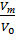 =0.99; ίкр=
=0.99; ίкр= 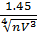 ; N=0.896
; N=0.896 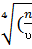 )3; dз=1.29
)3; dз=1.29